Bài tập về hai đường thẳng cắt nhau theo một góc bất kì

1. Các câu đúng là: b, c

    Các câu sai là: a

2. 

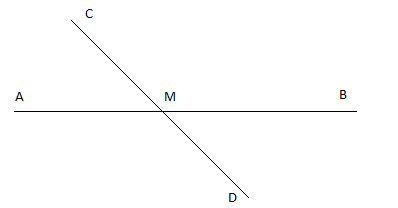
$\widehat{BMC}$ và $\widehat{CMA}$ là hai góc kề bù nên:

$\widehat{BMC}+\widehat{CMA}=180^{\circ}$

Mà $\widehat{BMC}=3\widehat{CMA}$ $\Rightarrow 4\widehat{CMA} = 180^{\circ}$

$\Rightarrow \widehat{CMA} = 45^{\circ}$ ; $\widehat{BMC}=3\widehat{CMA}=135^{\circ}$

Theo tính chất hai góc đối đỉnh ta có:

$\widehat{BMC}=\widehat{DMA}=135^{\circ}$

$\widehat{CMA}=\widehat{BMD}=45^{\circ}$

3. 

a) Tổng ba góc $\widehat{AOC}+\widehat{COD}+\widehat{DOB}=180^{\circ}$ (do A, O, B thẳng hàng)

Mà $\widehat{AOC}=\widehat{COD}=\widehat{DOB}$ (giả thiết)

$\Rightarrow \widehat{AOC}=\widehat{COD}=\widehat{DOB}=60^{\circ}$

- Tia OC chia góc $\widehat{AOD}$ thành hai góc bằng nhau, mỗi góc $60^{\circ}$ 

Vậy tia OC là tia phân giác của góc $\widehat{AOD}$

b) Tia OD chia góc $\widehat{BOC}$ thành hai góc bằng nhau, mỗi góc $60^{\circ}$ 

Vậy tia OD là tia phân giác của $\widehat{BOC}$

c) Ta có: $\widehat{BOC}=120^{\circ}$ (theo cách tính trên); $\widehat{BOE}=60^{\circ}$ (theo giả thiết)

Vậy $\widehat{BOC}+\widehat{BOE} = 180^{\circ}$

$\Rightarrow $ C, O, E nằm trên một đường thẳng.

Suy ra OE là tia đối của tia OC. Vậy hai góc $\widehat{AOC}$ và $\widehat{BOE}$ là hai góc đối đỉnh.

d) Ta có: $\widehat{BOD}=60^{\circ}$; $\widehat{BOE}=60^{\circ}$

Mà OB nằm giữa hai tia OD, OE và $\widehat{BOD}=\widehat{BOE}$

$\Rightarrow $ OB là tia phân giác của $\widehat{DOE}$