A. PHƯƠNG PHÁP GIẢI

- Nếu $\Delta $ABC vuông có độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c thì $a^{2}=b^{2}+c^{2}$

Ý nghĩa: Diện tích hình vuông có cạnh bằng độ dài cạnh huyền bằng tổng diện tích hai hình vuông có cạnh bằng độ dài hai cạnh góc vuông

Từ định lí đảo ta thấy: Nếu một tam giác có ba cạnh độ dài tỉ lệ với 3 : 4 : 5 thì tam giác đó vuông.

Ứng dụng kết quả này để đoán góc vuông hoặc kiểm tra một góc có bằng $90^{\circ}$ không.

- Ứng dụng:

• Từ định lí: Trong một tam giác vuông biết độ dài hai cạnh thì tính được cạnh thứ ba.
• Để chứng minh hai đường thẳng vuông góc với nhau.

Ví dụ 1: Cho $\Delta $ABC đường vuông góc hạ từ A xuống BC là AH. Biết AH = 6cm, BH = 4,5cm, HC = 8cm. Hỏi tam giác ABC là tam giác gì?

Hướng dẫn:

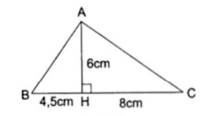
Xét $\Delta $AHC là tam giác vuông tại H. Theo định lí Py-ta-go ta có:

$AC^{2}=AH^{2}+HC^{2}=6^{2}+8^{2}=100$

Xét $\Delta $ABH vuông tại H. Theo định lí Py-ta-go ta có:

$AB^{2}=AH^{2}+HB^{2}=6^{2}+(4,5)^{2}=56,25$

Vậy $AC^{2}+AB^{2}=100+56,25=156,25$

Mà BC = BH + HC = 4,5 + 8 = 12,5 $\Rightarrow BC^{2}=12,5^{2}=156,25$

$\Rightarrow AC^{2}+AB^{2} = BC^{2}$

Theo định lí Py-ta-go ta thấy $\Delta $ABC vuông tại A.

Ví dụ 2: Cho $\Delta $ABC nhọn. Kẻ AH $\perp $ BC. Biết độ dài các cạnh AC = 15cm, AH = 12cm và BH = 9cm. Hỏi $\Delta $ABC là tam giác gì? So sánh BH và CH.

Hướng dẫn:

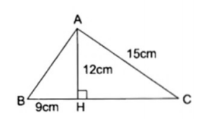
Xét $\Delta $AHC vuông tại H 

Theo định lý Py-ta-go ta có:

$AC^{2}=AH^{2}+HC^{2}\Rightarrow 15^{2}=12^{2}+HC^{2}$

$\Rightarrow HC^{2}=15^{2}-12^{2}=81$

$\Leftrightarrow HC = 9$ (cm)

Xét $\Delta $ABH vuông tại H, theo định lí Py-ta-go ta có:

$AB^{2}=AH^{2}+BH^{2}\Leftrightarrow AB^{2}=12^{2}+9^{2}=225$

$\Leftrightarrow AB=15$ (cm) 

Vậy $\Delta $ABC có AB = AC nên $\Delta $ABC cân tại A.

Ta cũng có BH = HC = 9 (cm)