A. PHƯƠNG PHÁP GIẢI

- Muốn chứng tỏ d là đường trung trực của đoạn thẳng MN ta phải chứng tỏ nó thỏa mãn cả hai điều kiện:

• Đường thẳng d qua I trong đó MI = IN (I nằm giữa M và N)
• Đường thẳng d $\perp $ MN ($\widehat{MId}=90^{\circ}$)
• Cách vẽ: Chẳng hạn vẽ đường trung trực của đoạn thẳng AB cho trước.

Cách 1: Dùng êke

Bước 1: Tìm I là trung điểm của đoạn thẳng AB.

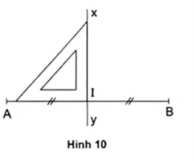
Bước 2: Đặt êke sao cho: Một cạnh góc vuông trùng với đoạn thẳng AB. Đỉnh góc vuông của êke trùng với điểm I.

Bước 3: Kẻ đường thẳng theo cạnh góc vuông thứ hai của êke

Ta có xy là đường trung trực của đoạn thẳng AB (hình 10)

Cách 2: Dùng thước đo góc.

Bước 1: Như trên

Bước 2: Đặt thước đo góc sao cho cạnh của thước trùng với đoạn thẳng AB. Tâm của thước trùng với điểm I.

Bước 3: Đánh dấu vạch 90$^{\circ}$ và nối điểm đó với I (hình 11)

Ví dụ 1: Trên tia Ox ta đặt các điểm M, N, I và P sao cho OP = 2OM; ON = $\frac{1}{4}$OP ; OI = 3ON. Biết OP = 10cm

a) Tìm độ dài các đoạn OI, OM, ON

b) Xác định vị trí các điểm M, N, I, P trên tia Ox (theo thứ tự nào)

c) Từ điểm Q thuộc nửa mặt phẳng bờ là Ox, biết QM $\perp $ Ox. Nối các điểm QO, QP QI, QN. Vậy tia QM nằm giữa hai tia nào? Tại sao?

d) QM là đường trung trực của đoạn thẳng nào? Tại sao?

Hướng dẫn:

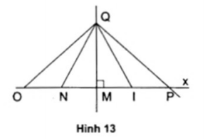
a) OP = 10cm và OP = 2OM. Suy ra OM = 5cm

    ON = $\frac{1}{4}$OP = $\frac{1}{4}$.10 = 2,5cm ; OI = 3ON = 3.2,5 = 7,5cm.

b) Các tia OP, OM, ON, OI có chung gốc O , ON = 2,5cm; OM = 5cm; OI = 7,5cm; OP = 10cm

Do đó ON < OM < OI < OP

Suy ra 4 điểm nằm trên Ox theo thứ tự N, M, I, P.

c) Theo thứ tự trên ta có:

- M nằm giữa hai điểm N và I nên tia QM nằm giữa hai tia QN và QI

- M nằm giữa hai điểm N và P nên tia QM nằm giữa hai tia QN và QP

- M nằm giữa hai điểm O và I nên tia QM nằm giữa hai tia QO và QI

- M nằm giữa hai điểm O và P nên tia QM nằm giữa hai tia QO và QP

d) Theo câu b) ta có M nằm giữa O và P

$\Rightarrow $ OM + MP = OP

$\Rightarrow $ MP = OP - OM = 10 - 5 = 5 (cm)

Do đó MP = OM = 5 (cm)
Mà QM $\perp $ NM tại M (đề bài)

Suy ra QM là đường trung trực của đoạn thẳng OP.

 Vì N nằm giữa O và M nên ON + NM = OM

$\Rightarrow $ NM = OM - ON = 5 - 2,5 = 2,5 (cm)

 Vì M nằm giữa O và I nên OM + MI = OI

$\Rightarrow $ MI = OI - OM = 7,5 - 5 = 2,5 (cm)

Do đó MI = NM

Mà QM $\perp $ OP tại M (đề bài)

Suy ra QM là đường trung trực của đoạn thẳng NI