A. PHƯƠNG PHÁP GIẢI

1. Hai đường thẳng cắt nhau theo một góc bất kì

- Biết cách vẽ và nhận ra hai góc đối đỉnh theo cách nhanh nhất.

Chú ý: Hai góc đối đỉnh thì bằng nhau, nhưng điều ngược lại thì không đúng (nên không được áp dụng).

Chẳng hạn hai góc trong hình a, b, c, d bằng nhau nhưng không phải là hai góc đối đỉnh.

- Hai đường thẳng cắt nhau tại một điểm tạo thành bốn góc (không kể các góc bẹt) có chung đỉnh tại điểm cắt.

• Nếu biết số đo của một góc thì dựa vào tính chất của hai góc kề bù nhau và tính chất hai góc đối đỉnh, ta tính được số đo của ba góc còn lại.
• Ngược lại nếu cho hai góc bằng nhau và có một cặp cạnh là hai tia đối của nhau, bằng cách tính toán ta có thể chứng tỏ được cặp cạnh thứ hai cũng là hai tia đối nhau để suy ra hai góc đó là hai góc đối đỉnh.

Thật vậy: $\widehat{AOB}=\widehat{COD}=a^{\circ}$ ($0^{\circ}<a^{\circ}<180^{\circ}$); OA và OC là hai tia đối nhau. Chứng tỏ hai tia OB và OD cũng là hai tia đối nhau.

Hai tia OA và OC đối nhau (theo giả thiết) vậy A, C, O  nằm trên một đường thẳng. Xét nửa mặt phẳng bờ là đường thẳng AC chứa tia OD, có:

$\widehat{AOD}=180^{\circ}-a^{\circ}$ (hai góc kề bù)

Vậy $\widehat{AOB}+\widehat{AOD}=a^{\circ}+180^{\circ}-a^{\circ} = 180^{\circ}$, suy ra $\widehat{BOD} = 180^{\circ}$ $\Rightarrow $ Tia OB và OD thuộc một đường thẳng. Suy ra OB và OD là hai tia đối nhau.

Suy ra $\widehat{AOB}$ và $\widehat{COD}$ có chung đỉnh O có hai cặp cạnh là hai tia đối nhau, vậy nó là hai góc đối đỉnh.

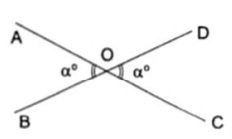
Ví dụ 1: Cho hai đường thẳng AB và CD cắt nhau tại O.

a) Kể tên các cặp góc đối đỉnh (không kể góc bẹt)

b) Biết số đo của góc $\widehat{AOC} = 40^{\circ}$. Tính các góc còn lại.

Hướng dẫn:

a) Các cặp góc đối đỉnh là:

• $\widehat{AOC}$ và $\widehat{BOD}$
• $\widehat{AOD}$ và $\widehat{COB}$

b) Do $\widehat{AOC}$ và $\widehat{COB}$ là hai góc kề bù nên:

$\widehat{AOC}$ + $\widehat{COB}$ = $180^{\circ}$

Theo đề bài: $\widehat{AOC}=40^{\circ}$ 

$\Rightarrow \widehat{COB} = 180^{\circ} - 40^{\circ}=140^{\circ}$

Do đó ta có:

$\widehat{AOC} = 40^{\circ} = \widehat{BOD}$

$\widehat{COB}=40^{\circ} = \widehat{COB}$

2. Hai đường thẳng cắt nhau có góc tạo thành là góc vuông

- Sử dựng thước thẳng và eke để vẽ chính xác: đường thẳng a' $\perp $ a và viết kí hiệu.

- Làm quen sử dụng thước thẳng kẻ hai đường thẳng vuông góc bằng cách ước lượng (tương đối chính xác)

-  Sử dụng thước thẳng và êke vẽ thánh thạo hai đường thẳng vuông góc trong các trường hợp:

• Đường thẳng a và điểm O thuộc a. Vẽ đường thẳng a' $\perp $ a và qua O.
• Đường thẳng qua a và điểm O ngoài đường thẳng a. Vẽ đường thẳng a' $\perp $ a và qua O.

- Tập kiểm tra xem hai đường thẳng có vuông góc với nhau không.

• Bằng êke
• Bằng cách gấp tờ giấy
• Bằng cách ước lương

Ví dụ 2: Đường thẳng AB và đường thẳng MN cắt nhau tại O sao cho góc $\widehat{AOM}$ là góc tù. Tại O kẻ đường thẳng CD $\perp $ AB và đường thẳng EF $\perp $ MN.

a) Hãy chứng tỏ $\widehat{AOE}=\widehat{MOC}$

b) Trong hình vừa vẽ ta thấy có tám góc nhọn. Hãy chứng tỏ tám góc nhọn đó có thể được chia làm hai nhóm, mỗi nhóm có bốn góc nhọn bẳng nhau.

Hướng dẫn:

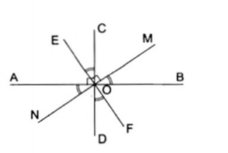
a) Ta có: $\widehat{AOE}=\widehat{AOM}-90^{\circ}$

       $\widehat{MOC}=\widehat{AOM}-90^{\circ}$

$\Rightarrow \widehat{AOE} = \widehat{MOC}$

b) Ta có: $\widehat{AOE} = \widehat{BOF}$ (hai góc đối đỉnh)

               $\widehat{MOC} = \widehat{DON}$ (hai góc đối đỉnh)

$\Rightarrow \widehat{AOE} = \widehat{BOF}=\widehat{MOC} = \widehat{DON}$

Mà: $\widehat{AOE}+\widehat{COE}=90^{\circ}$ (theo đề bài)

    $\widehat{AOE}+\widehat{AON}=90^{\circ}$ (theo đề bài)

$\Rightarrow \widehat{COE} = \widehat{AON}$

Mà $\widehat{COE} = \widehat{DOF}$ (hai góc đối đỉnh)

   $\widehat{AON} = \widehat{MOB}$ (hai góc đối đỉnh)

$\Rightarrow \widehat{COE} = \widehat{AON}=\widehat{DOF} = \widehat{MOB}$