A. PHƯƠNG PHÁP GIẢI

- Từ các bất đẳng thức trong tam giác đã nêu ta có thể kiểm tra độ dài ba cạnh có thỏa mãn bất đẳng thức hay không theo cách nhanh nhất là:

• Chọn cạnh lớn nhất xem có nhỏ hơn tổng hai cạnh còn lại không?
• Hoặc chọn cạnh bé nhất xem có lớn hơn hiệu hai cạnh còn lại không?

Chẳng hạn: Có thể dựng tam giác có ba cạnh có độ dài như sau không:

a) 6cm; 3cm; 2cm

b) 3cm; 4cm; 6cm

Trả lời:

a) Không được vì 6 > 3 + 2

b) Được vì 6 < 3 + 4; 3 > 6 - 4

- Ứng dụng của bất đẳng thức:

• Để só sánh các đoạn thẳng không bằng nhau.
• Để tìm điều kiện cho một tam giác tồn tại

- Chú ý: Ở đây sử dụng kiến thức bất đẳng thức mà học sinh chưa được học trong đại số, nên lưu ý:

• Độ dài các cạnh của tam giác là các số dương.
• Nếu cộng hai vế thì hai bất đẳng thức phải cùng chiều (cùng > hoặc cùng <)
• Nếu một vế có dạng: AB - CD thì cần có điều kiện AB $\geq $ CD để AB - CD $\geq $ 0.

Ví dụ 1: Cho góc nhọn $\widehat{xOy}$. Trên Ox lấy hai điểm M và N (điểm M nằm giữa hai điểm C và N), trên Oy lấy hai điểm E và F (điểm E nằm giữa 2 điểm O và F). Chứng minh rằng MN + EF < MF + NE.

Hướng dẫn:

Gọi I là giao điểm của MF và NE

Xét $\Delta $MIN có: MN < MI + IN (tổng hai cạnh lớn hơn cạnh còn lại)

Xét $\Delta $efi có: EF < EI + IF (tổng hai cạnh lớn hơn cạnh còn lại)

$\Rightarrow $ MN + EF + MI < MI + IN + EI + IF

$\Leftrightarrow  MN + EF + MI < (MI + IF) + (EI + IN)

Hay MN + EF + MI < MF + NE

Ví dụ 2: Cho $\Delta $ABC có AB > AC. Gọi M là trung điểm của cạnh BC, nối AM. Chứng minh rằng $\frac{AB - AC}{2}<AM<\frac{AB +AC}{2}$

Hướng dẫn:

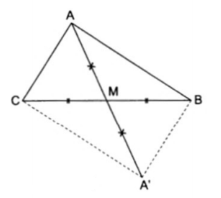
Trên tia đối của tia MA lấy điểm A' sao cho MA' = MA

Xét $\Delta $ABM và $\Delta $A'MC có:

AM = MA'

BM = MC

$\widehat{AMB}=\widehat{CMA'}$

$\Rightarrow $ $\Delta $ABM = $\Delta $A'MC (c.g.c)

$\Rightarrow $ AB = A'C

Xét $\Delta $ACA' có: CA' - CA < AA' < AC + CA'

AB > AC $\Rightarrow $ AB - AC > 0 mà AB = CA'

Do đó CA' - CA > 0; AA' = 2AM

$\Rightarrow $ AB - AC < 2AM < AB + AC

Hay $\frac{AB - AC}{2}<AM<\frac{AB +AC}{2}$