A. PHƯƠNG PHÁP GIẢI

- Giao điểm ba đường trung trực cách đều ba đỉnh. Vì vậy nếu O là giao điểm ba đường trung trực của $\Delta $ABC thì đường tròn (O; OA) sẽ đi qua B và C.

- Trong tam giác cân thì đường phân giác của góc ở đỉnh vừa là đường trung tuyến, vửa là đường trung trực của cạnh đáy.

- Cách tìm giao điểm ba đường trung trực của một tam giác: vẽ hai đường trung trực của hai cạnh

Ví dụ 1: Cho $\Delta $ABC cân tại A, phân giác AH. Đường trung trực của cạnh AB cắt đường AH tại O. Trên các cạnh AB và AC của tam giác ấy lấy các điểm E và F sao cho AE + AF = AB.

a) Chứng minh OE = OF

b) Chứng minh khi E và F di động trên cạnh AB và AC của $\Delta $ABC nhưng luôn có AE + AF = AB thì hai đường trung trực của EF đi qua một điểm cố định

c) Tìm vị trí của E và F để O là trung điểm của EF.

Hướng dẫn:

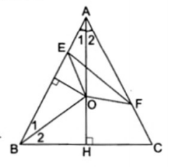
a) AE + AF = AB

   AE + EB = AB

$\Rightarrow $ AF = EB

Có $\widehat{A_{1}}=\widehat{A_{2}}$

Vì O nằm trên đường trung trực của AB nên $\Delta $OAB cân tại O do đó $\widehat{A_{1}}=\widehat{B_{1}}$ , OB = OA

$\Rightarrow $ $\widehat{A_{2}}=\widehat{B_{1}}$ (= $\widehat{A_{1}}$)

Xét $\Delta $BOE và $\Delta $AOF có:

AF = BE

$\widehat{A_{2}}=\widehat{B_{1}}$

OB = OA

$\Rightarrow $ $\Delta $BOE = $\Delta $AOF

$\Rightarrow $ OE = OF

b) Vì OE = OF nên O nằm trên đường trung trực của OF.

Mà AB và BC cố định, O là giao điểm của hai đường trung trực cố định đó nên O là điểm cố định. Vậy E và F di động nhưng trung trực của EF luôn đi qua điểm cố định O.

c) Theo câu a ta có OE = OF, vậy để O là trung điểm của EF thì E, O, F thẳng hàng.

Khi đó AE = AF = $\frac{1}{2}$AB.