Bài tập về tính chất ba đường trung trực của tam giác

1.

$\Delta $ABC có $\widehat{A}=90^{\circ}$. Lấy M là trung điểm cạnh BC.

Ta chứng minh được MA = MB = MC = $\frac{1}{2}$BC

MA = MB nên M nằm trên đường trung trực của AB

MA = MC nên M nằm trên đường trung trực của AC

MC = MB nên M nằm trên đường trung trực của BC

Vậy M là giao điểm của ba đường trung trực của $\Delta $ABC

2.

a) Xét $\Delta $AOP có: Ox là đường trung trực của AP nên OA = OP

$\Delta $AOP cân tại O $\Rightarrow $ OI vừa là đường trung trực vừa là đường phân giác của $\widehat{O}$

$\Rightarrow \widehat{O_{1}}=\widehat{O_{2}}$

Tương tự:

Xét $\Delta $BOP có: Oy là đường trung trực của BP nên OB = OP

$\Delta $AOP cân tại O $\Rightarrow $ OE vừa là đường trung trực vừa là đường phân giác của $\widehat{O}$

$\Rightarrow \widehat{O_{3}}=\widehat{O_{4}}$

$\Rightarrow $ $\widehat{O_{1}}+\widehat{O_{4}}=\widehat{O_{2}}+\widehat{O_{3}}$

Mà $\widehat{O_{2}}+\widehat{O_{3}}=90^{\circ}$

$\Rightarrow \widehat{O_{1}}+\widehat{O_{4}}+\widehat{O_{2}}+\widehat{O_{3}}=180^{\circ}$

$\Rightarrow \widehat{AOB}=180^{\circ}$ hay A, O, B thẳng hàng.

b) Theo câu a ta có:

$\Delta $AOP cân tại O nên $\widehat{A}=\widehat{P_{1}}$

$\Delta $BOP cân tại O nên $\widehat{B}=\widehat{P_{2}}$

$\Rightarrow \widehat{A}+\widehat{B}=\widehat{P_{1}}+\widehat{P_{2}}$

Do A, O, B thẳng hàng nên AB là một cạnh của $\Delta $APB

Từ đó $\widehat{A}+\widehat{B}+\widehat{P_{1}}+\widehat{P_{2}}=180^{\circ}$

$\Leftrightarrow \widehat{A}+\widehat{B}=\widehat{P_{1}}+\widehat{P_{2}}=90^{\circ}$

Vậy $\Delta $BAP vuông tai P có O là trung điểm cạnh huyền AB.

Từ đó ta chứng minh được O là trung điểm ba đường trung trực của $\Delta $APB (theo bài 1)

3.

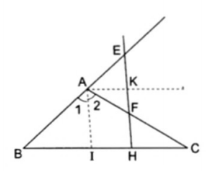
a) Xét $\Delta $AEF có :

$\widehat{E}=\widehat{A_{1}}$ (2 góc đồng vị)

$\widehat{F}=\widehat{A_{2}}$ (2 góc so le trong)

Mà $\widehat{A_{1}}=\widehat{A_{2}}\Rightarrow \widehat{E}=\widehat{F}$ 

$\Rightarrow $ $\Delta $AEF cân tại A.

b) Gọi K là giao điểm của EH với đường trung trực của EF.

$\Delta $AEF cân tại A nên AK vừa là đường trung trực, vừa là đường phân giác của góc $\widehat{EAF}$.

Mà $\widehat{BAC}$ và $\widehat{CAF}$ là hai góc kề bù có AI và AK là hai đường phân giác nên AI $\perp $ AK.

c) $\Delta $ABC cố định nên đường phân giác AI cố định, AK $\perp $ AI nên AI cũng cố định. Điểm H chuyển động trên IC thì $\Delta $EAF luôn cân tại A nên đường trung trực qua A cố định.

4.

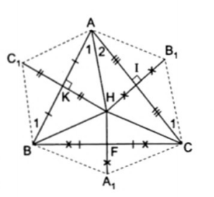
Xét $\Delta $AKH và $\Delta $BKC₁ là hai tam giác vuông có:

AK = KB

KH = KC₁

$\Rightarrow $ $\Delta $AKH = $\Delta $BKC₁ (hai cạnh góc vuông)

$\Rightarrow $ AH = BC₁    (1)

Và $\widehat{A_{1}}=\widehat{B_{1}}\Rightarrow $ AH // BC₁ (có hai góc so le trong bằng nhau)   (2)

Xét $\Delta $AHI và $\Delta $CB₁I là hai tam giác vuông có:

HI = IB

AI = IC

$\Rightarrow $ $\Delta $AHI = $\Delta $CB₁I   (3)

Và $\widehat{A_{2}}=\widehat{C_{1}}\Rightarrow $ AH // B₁C    (4)

Từ (1) và (3) $\Rightarrow $ BC₁ // CB₁

Từ (2) và (4) $\Rightarrow $ BC₁ = CB₁ = AH

Tương tự ta có AC₁ // A₁C; A₁B // AB₁

                             AC₁ = A₁C = BH; A₁B // AB₁ = CH

Mà H là giao điểm ba đường trung trực của $\Delta $ABC nên AH = BH = CH

Do đó BC₁ = B₁C = AC₁ = A₁C = AB₁ = A₁B

b) Xét $\Delta $C₁AB₁ và $\Delta $CA₁B là hai tam giác cân, ta có:

C₁A = CA₁ 

AB₁ = BA₁

$\widehat{C_{1}AB_{1}}=\widehat{CA_{1}B}$

$\Rightarrow $ $\Delta $C₁AB₁ = $\Delta $CA₁B (c.g.c)

$\Rightarrow $  BC = B₁C₁ 

Tương tự ta có: AC = A₁C₁

                AB = A₁B₁

Do đó $\Delta $ABC = $\Delta $A₁B₁C₁ (c.c.c)