A. PHƯƠNG PHÁP GIẢI

- Đến đây ta có thêm một dấu hiệu nhận biết hai đường thẳng song song là:

• Nếu hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song.
• Hoặc nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

- Cần làm quen việc vẽ bằng tay (không cần êke) nhanh nhưng tương đối chính xác: 2 đường thẳng song song, hai đường thẳng vuông góc để sử dụng khi làm nháp (đỡ mất thời gian)

- Để dễ nhận ra hai góc có cạnh tương ứng song song hay hai góc có cạnh tương ứng vuông góc, ta thực hiện theo các bước sau:

Bước 1: Chỉ ra hai cạnh của góc này và hai cạnh của góc kia

Bước 2: Từ đó dựa theo đầu bài để xem quan hệ tương ứng giữa chúng (có thể đầu bài cho trực tiếp, có thể phải suy diễn từ đầu bài, tập nhận xét để tìm lời giải)

- Quan hệ giữa tính song song và vuông góc ở đây là:

• Nếu c $\perp $ a và c $\perp $ b thì kết luận a // b (sử dụng vuông góc để kết luận song song)
• Hoặc nếu a $\perp $ c và a // b thì kết luận b $\perp $ c

Ví dụ 1: Cho $\widehat{xOy}$ và $\widehat{yOz}$ là hai góc kề bù nhau OE và OF là hai tia phân giác của hai góc $\widehat{xOy}$ và $\widehat{yOz}$. Trên OF lấy điểm H. Tại H kẻ đường thẳng vuông góc với OF cắt Oy tại M và Oz tại N. Chứng tỏ rằng $\Delta $MON có $\widehat{OMN}=\widehat{ONM}$.

Hướng dẫn:

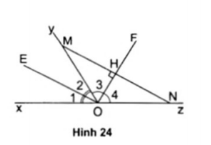
OE là tia phân giác $\widehat{xOy}$ nên $\widehat{O_{1}}=\widehat{O_{2}}$ (1)

OF là tia phân giác $\widehat{yOz}$ nên $\widehat{O_{4}}=\widehat{O_{3}}$ (2)

Từ (1) và (2) suy ra $\widehat{O_{1}}+\widehat{O_{4}}=\widehat{O_{2}}+\widehat{O_{3}}$

Mà $\widehat{O_{1}}+\widehat{O_{4}}+\widehat{O_{2}}+\widehat{O_{3}}=180^{\circ}$

Do đó $\widehat{O_{2}}+\widehat{O_{3}}=90^{\circ}$

$\Rightarrow OF\perp OF$

Ta có $OF\perp MN$ (theo đề bài) do đó OE // MN (do OE và MN cùng vuông góc với OF), suy ra $\widehat{O_{2}}=\widehat{OMN}$ (so le trong); $\widehat{O_{1}}=\widehat{ONM}$ (đồng vị)

Mà $\widehat{O_{1}}=\widehat{O_{2}}$ do đó $\widehat{OMN}=\widehat{ONM}$