Siêu nhanh giải bài 3 chương II toán 12 Chân trời sáng tạo tập 1
Giải siêu nhanh bài 3 chương II toán 12 Chân trời sáng tạo tập 1. Giải siêu nhanh toán 12 Chân trời sáng tạo tập 1. Những phần nào có thể rút gọn, lược bỏ và tóm gọn. Đều được áp dụng vào bài giải này. Thêm cách giải mới để học sinh lựa chọn. Để tìm ra phong cách học toán 12 Chân trời sáng tạo tập 1 phù hợp với mình.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 3: BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ
1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
Khởi động 1: Trong không gian ![]() , có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trong mặt phẳng
, có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trong mặt phẳng ![]() không?
không?
![]()
![]()
Giải rút gọn:
Trong không gian ![]() , ta có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trên mặt phẳng tọa độ.
, ta có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trên mặt phẳng tọa độ.
Khám phá 1: Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() ,
, ![]() với số thực
với số thực ![]() .
.
a) Biểu diễn từng vectơ ![]() theo ba vectơ
theo ba vectơ ![]() .
.
b) Biểu diễn các vectơ ![]() theo ba vectơ
theo ba vectơ ![]() , từ đó suy ra tọa độ của các vectơ
, từ đó suy ra tọa độ của các vectơ![]()
Giải rút gọn:
a) ![]() ;
;![]()
b)![]()
Và ![]()
Và ![]()
Thực hành 1: Cho ba vectơ![]()
a) Tìm tọa độ của vectơ 
b) Tìm tọa độ của vectơ ![]()
c) Chứng minh ![]() cùng phương với vectơ
cùng phương với vectơ ![]()
Giải rút gọn:
a) Ta có: 
Khi đó 
b) Ta có ![]()
Suy ra ![]()
c) Ta có ![]() .
.
Vậy ![]() cùng phương với
cùng phương với ![]()
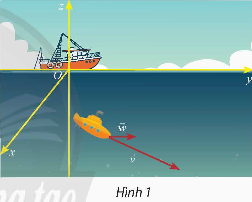
Vận dụng 1: Một thiết bị thăm dò đáy biển đang lặn với vận tốc ![]() (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là
(Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là ![]() .
.
a) Tìm tọa độ của vectơ tổng hai vận tốc ![]()
b) Giả sử thiết bị thăm dò lặn với vận tốc ![]() , hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.
, hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.
Giải rút gọn:
a) ![]()
b) Ta có: ![]() . Vậy vectơ vận tốc của thiết bị thăm dò cùng hướng với vectơ vận tốc của dòng hải lưu.
. Vậy vectơ vận tốc của thiết bị thăm dò cùng hướng với vectơ vận tốc của dòng hải lưu.
2. BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG
Khám phá 2: Cho hai vectơ ![]() ,
, ![]() .
.
a) Biểu diễn từng vectơ ![]() theo ba vectơ
theo ba vectơ ![]() .
.
b) Tính các tích vô hướng ![]() .
.
c) Tính tích vô hướng ![]() theo tọa độ của hai vectơ
theo tọa độ của hai vectơ![]()
Giải rút gọn:
a) ![]() ;
; ![]()
b) ![]() ;
; ![]()
c) ![]() =
= ![]() ).
). ![]() =
= ![]()
Thực hành 2: Cho ba vectơ![]()
a) Tính ![]() .
.
b) Tính ![]() .
.
c) Cho ![]() . Vectơ
. Vectơ ![]() có vuông góc với
có vuông góc với ![]() không?
không?
Giải rút gọn:
a) ![]() ;
;
![]()
b) ![]() =
= ![]() ;
; ![]() =
=![]()
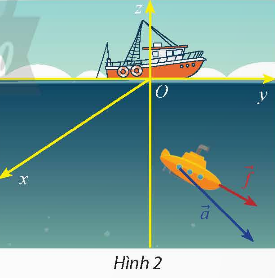
Vận dụng 2: Một thiết bị dò thăm đáy biển (HÌnh 2) được đẩy bởi lực ![]() (đơn vị: N) giúp thiết bị thực hiện độ dời
(đơn vị: N) giúp thiết bị thực hiện độ dời ![]() (đơn vị: m). Tính công lực sinh bởi lực
(đơn vị: m). Tính công lực sinh bởi lực ![]() .
.
Giải rút gọn:
Công sinh ra bởi lực ![]() khi thực hiện độ dời
khi thực hiện độ dời ![]() là:
là:
![]() (N)
(N)
3. VẬN DỤNG
Khám phá 3: Cho hai điểm ![]() . Từ biểu thức
. Từ biểu thức ![]() , tìm tọa độ của vectơ
, tìm tọa độ của vectơ ![]() theo tọa độ hai điểm
theo tọa độ hai điểm ![]() và
và ![]() .
.
Giải rút gọn:
Ta có: ![]() ;
;![]() .
.
Nên ![]()
Thực hành 3: Cho ba điểm ![]() .
.
a) Tìm tọa độ của các vectơ ![]()
b) Tính các độ dài ![]() .
.
Giải rút gọn:
a) ![]() ;
;
![]() ;
;
![]() .
.
b)![]()
![]()
![]()
Khám phá 4: Cho tam giác ![]() có
có ![]() . Gọi
. Gọi ![]() là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng ![]() và
và ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() .
.
Sử dụng các hệ thức vectơ  , tìm tọa độ của các điểm
, tìm tọa độ của các điểm ![]() và
và ![]() .
.
Giải rút gọn:
Ta có ![]()
Ta có 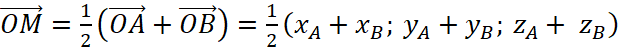
Hay 
Nên 
Tương tự, ta có 
Nên 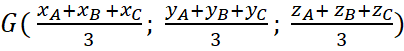
Thực hành 4: Cho tam giác ![]() có
có ![]() . Tìm tọa độ:
. Tìm tọa độ:
a) Các điểm ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() ;
;
b) Trọng tâm ![]() của tam giác
của tam giác ![]() .
.
Giải rút gọn:
a) Tọa độ trung điểm ![]() của cạnh
của cạnh ![]() là
là 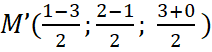 hay
hay 
Tọa độ trung điểm ![]() của cạnh
của cạnh ![]() là
là 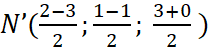 hay
hay 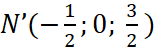
Tọa độ trung điểm ![]() của cạnh
của cạnh ![]() là
là 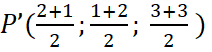 hay
hay 
b) Tọa độ trọng tâm ![]() là:
là: 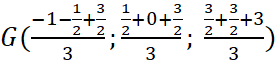 hay
hay 
Vận dụng 3: Cho hình chóp ![]() có
có ![]() ,
, ![]() và đáy
và đáy ![]() là tam giác đều cạnh a,
là tam giác đều cạnh a, ![]() là trung điểm của
là trung điểm của ![]() . Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:
. Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:
a) Các điểm ![]() .
.
b) Trung điểm ![]() của
của ![]() và trung điểm
và trung điểm ![]() của
của ![]() .
.
c) Trọng tâm ![]() của tam giác
của tam giác ![]() .
.
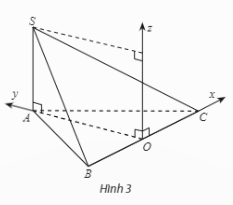
Giải rút gọn:
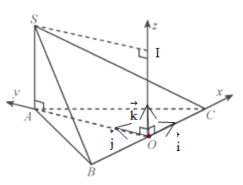
a) Vì ![]() là tam giác đều cạnh a,
là tam giác đều cạnh a, ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]() là đường cao. Từ đó suy ra
là đường cao. Từ đó suy ra  và
và ![]()
→ 
Gọi ![]() là hình chiếu của
là hình chiếu của ![]() trên
trên ![]() . Ta có
. Ta có ![]() , vì
, vì ![]() cùng hướng với
cùng hướng với ![]() nên
nên ![]()
Áp dụng quy tắc hình bình hành, ta có: 
→ 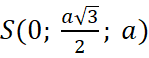
b) Tọa độ trung điểm ![]() của
của ![]() là
là  hay
hay 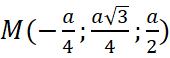
Tọa độ trung điểm ![]() của
của ![]() là
là  hay
hay 
c) Tọa độ của trọng tâm ![]() tam giác
tam giác ![]() là:
là:
 hay
hay 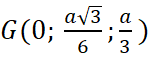
Thực hành 5: Cho tam giác ![]() có
có ![]() .
.
a) Tìm tọa độ điểm ![]() là chân đường cao kẻ từ
là chân đường cao kẻ từ ![]() của tam giác
của tam giác ![]() .
.
b) Tìm độ dài cạnh ![]() và
và ![]() .
.
c) Tính góc ![]() .
.
Giải rút gọn:

a) Ta có ![]() .
.
Vì ![]() là chân đường vuông góc kẻ từ
là chân đường vuông góc kẻ từ ![]() xuống
xuống ![]() nên
nên ![]() và
và ![]() .
.
Gọi ![]() , ta có
, ta có ![]() .
.
Vì ![]() và
và ![]() cùng phương nên tồn tại
cùng phương nên tồn tại ![]() sao cho
sao cho ![]() .
.
Do đó ![]()
![]() .
.
Vì vậy ![]() .
.
Khi đó ![]() .
.
Vì ![]() nên
nên ![]() .
.
Vậy 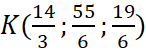 .
.
b) Ta có ![]() .
.
Vậy độ dài cạnh ![]() và
và ![]() là:
là:
![]()
c) Ta có: 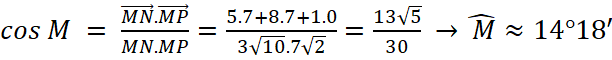
Vận dụng 4: Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian ![]() , một đội gồm ba drone giao hàng
, một đội gồm ba drone giao hàng ![]() đang có tọa độ là
đang có tọa độ là ![]() ,
, ![]() ,
, ![]() . Tính:
. Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc ![]() .
.
Giải rút gọn:
a) Ta có ![]() .
.
Khi đó: ![]() và
và ![]()
b) Ta có 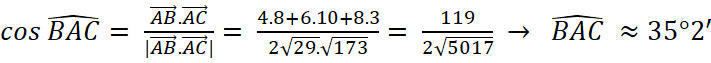
4. GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA
Giải rút gọn bài 1 trang 64 sách toán 12 tập 1 ctst: Tính:
a) ![]()
b) ![]()
Giải rút gọn:
a) ![]()
b) ![]()
Giải rút gọn bài 2 trang 64 sách toán 12 tập 1 ctst Cho hai vectơ ![]() và
và ![]() . Tính tọa độ của vectơ
. Tính tọa độ của vectơ 
Giải rút gọn:
Có: 
Vậy tọa độ của vectơ  là:
là:
 hay
hay 
Giải rút gọn bài 3 trang 64 sách toán 12 tập 1 ctst: Cho ba điểm ![]() và
và ![]() .
.
a) Chứng minh ![]() là ba đỉnh của một tam giác. Tính chu vi tam giác
là ba đỉnh của một tam giác. Tính chu vi tam giác ![]() .
.
b) Tìm tọa độ trung điểm của các cạnh của tam giác ![]() .
.
c) Tìm tọa độ trọng tâm ![]() của tam giác
của tam giác ![]() .
.
Giải rút gọn:
a) Ta có ![]() . Vì
. Vì ![]() không có cùng phương nên
không có cùng phương nên ![]() không thẳng hàng. Vì vậy,
không thẳng hàng. Vì vậy, ![]() là ba đỉnh của một tam giác.
là ba đỉnh của một tam giác.
Chu vi tam giác ![]() là:
là:

=![]()
b) Gọi ![]() lần lượt là trung điểm của cạnh
lần lượt là trung điểm của cạnh ![]() .
.
Tọa độ điểm ![]() là
là 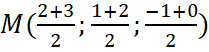 hay
hay 
Tọa độ điểm ![]() là
là  hay
hay 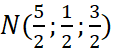
Tọa độ điểm ![]() là
là  hay
hay ![]()
c) Tọa độ trọng tâm ![]() của tam giác
của tam giác ![]() là
là  hay
hay 
Giải rút gọn bài 4 trang 64 sách toán 12 tập 1 ctst: Cho điểm ![]() . Hãy tìm tọa độ của các điểm:
. Hãy tìm tọa độ của các điểm:
a) ![]() lần lượt là hình chiếu vuông góc của M trên các mặt phẳng
lần lượt là hình chiếu vuông góc của M trên các mặt phẳng ![]() ,
, ![]() ,
, ![]() .
.
b) Gọi ![]() lần lượt là các điểm thỏa mãn:
lần lượt là các điểm thỏa mãn:
• ![]() là trung điểm của
là trung điểm của ![]() ;
;
• ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() tại điểm
tại điểm ![]() sao cho
sao cho ![]() là trung điểm của
là trung điểm của ![]() .
.
• ![]() vuông góc và cắt trục
vuông góc và cắt trục ![]() tại điểm
tại điểm ![]() sao cho
sao cho ![]() là trung điểm của
là trung điểm của ![]() .
.
Giải rút gọn:
a) Ta có ![]() ,
, ![]() ,
, ![]() .
.
b) ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]()
![]()
![]() .
.
Vậy ![]() .
.
Vì ![]() nên
nên ![]() .
.
Ta có ![]() .
.
![]() ⇒
⇒ ![]() ⇒
⇒ ![]()
⇒ ![]() ⇒
⇒ ![]()
Vì vậy ![]() .
.
Vì ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]()
![]()
![]() .
.
Vậy ![]() .
.
Vì ![]() nên
nên ![]() ⇒
⇒ ![]()
Vì ![]() ⇒
⇒ ![]() ⇔
⇔ ![]() ⇔
⇔ ![]() .
.
Vì ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]()
![]()
![]() .
.
Vậy ![]() .
.
Giải rút gọn bài 5 trang 64 sách toán 12 tập 1 ctst: Cho ba điểm ![]() ,
, ![]() và
và ![]() .
.
a) Tìm điểm ![]() trên trục
trên trục ![]() cách đều hai điểm
cách đều hai điểm ![]() .
.
b) Tìm điểm ![]() trên mặt phẳng
trên mặt phẳng ![]() cách đều ba điểm
cách đều ba điểm ![]() .
.
Giải rút gọn:
Vì ![]() nên
nên ![]() .
.
Vì ![]() cách đều hai điểm
cách đều hai điểm ![]() nên
nên ![]() hay
hay ![]()
![]()
![]()
 . Vậy
. Vậy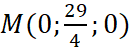
b) Vì ![]() nên
nên ![]() . Vì
. Vì ![]() cách đều ba điểm
cách đều ba điểm ![]() nên
nên ![]() hay
hay![]()
⇔ 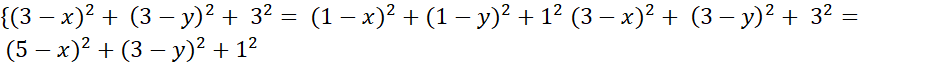
⇔![]() ⇔
⇔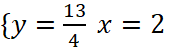 .
.
Vậy 
Giải rút gọn bài 6 trang 64 sách toán 12 tập 1 ctst: Cho các điểm ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Chứng minh rằng
. Chứng minh rằng ![]() là hình thang.
là hình thang.
Giải rút gọn:
Ta có: ![]() . Vì
. Vì ![]() nên
nên ![]() và
và ![]() cùng phương.
cùng phương.
Mặt khác, ![]() và
và ![]() không cùng phương nên
không cùng phương nên ![]() . Từ đó suy ra tứ giác
. Từ đó suy ra tứ giác ![]() là hình thang.
là hình thang.
Giải rút gọn bài 7 trang 64 sách toán 12 tập 1 ctst: Cho hình hộp ![]() có
có ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ các đỉnh còn lại của hình hộp.
. Tìm tọa độ các đỉnh còn lại của hình hộp.
Giải rút gọn:

a) Gọi ![]() là một đỉnh của hình hộp chữ nhật
là một đỉnh của hình hộp chữ nhật ![]() .
.
Ta có: ![]()
![]() . Vậy
. Vậy ![]() .
.
Ta có: ![]()
![]() . Vậy
. Vậy ![]() .
.
Ta có: ![]()
![]() . Vậy
. Vậy ![]() .
.
Ta có: ![]()
![]() . Vậy
. Vậy ![]() .
.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải toán 12 Chân trời sáng tạo tập 1 bài 3 chương II, Giải bài 3 chương II toán 12 Chân trời sáng tạo tập 1, Siêu nhanh giải bài 3 chương II toán 12 Chân trời sáng tạo tập 1
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận