Siêu nhanh giải bài 2 chương III toán 12 Chân trời sáng tạo tập 1
Giải siêu nhanh bài 2 chương III toán 12 Chân trời sáng tạo tập 1. Giải siêu nhanh toán 12 Chân trời sáng tạo tập 1. Những phần nào có thể rút gọn, lược bỏ và tóm gọn. Đều được áp dụng vào bài giải này. Thêm cách giải mới để học sinh lựa chọn. Để tìm ra phong cách học toán 12 Chân trời sáng tạo tập 1 phù hợp với mình.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 2: PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN CỦA MẪU SỐ LIỆU GHÉP NHÓM
Khám phá:

a) Trong biểu đồ ở hoạt động Khởi động, cột thứ nhất biểu diễn số lượng học sinh có chiều cao từ 160cm đến dưới 164cm; cột thứ hai biểu diễn số lượng học sinh có chiều cao từ 164cm đến dưới 168cm, …
Hãy lập bảng tần số ghép nhóm cho mẫu số liệu ở hoạt động Khởi động, xác định giá trị đại diện của mỗi nhóm và tính số trung bình của mẫu số liệu ghép nhóm.
b) Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của nhóm tương ứng. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu mới.
Giải rút gọn:
a)
Chiều cao (cm) | [160; 164) | [164; 168) | [168; 172) | [172; 176) | [176; 180) |
Số học sinh | 3 | 5 | 8 | 4 | 1 |
Giá trị đại diện | 162 | 166 | 170 | 174 | 178 |
b)
Số học sinh | 3 | 5 | 8 | 4 | 1 |
Giá trị đại diện | 162 | 166 | 170 | 174 | 178 |
Cỡ mẫu: n =21
Giá trị trung bình của mẫu số liệu mới là:
![]()
![]()
Phương sai của mẫu số liệu mới là:
![]()
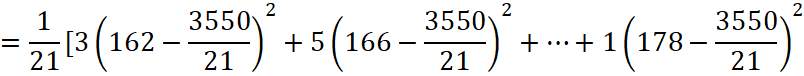
![]()
Độ lệch chuẩn của mẫu số liệu mới là: ![]()
Thực hành 1: Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm ở hoạt động Khởi động trang 75.
Chiều cao (cm) | [160; 164) | [164; 168) | [168; 172) | [172; 176) | [176; 180) |
Số học sinh | 3 | 5 | 8 | 4 | 1 |
Giải rút gọn:
Cỡ mẫu: n =21
Giá trị trung bình của mẫu số liệu ghép nhóm là:
![]()
![]()
Phương sai của mẫu số liệu ghép nhóm là:
![]()

![]()
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: ![]()
Thực hành 2: Mai và Ngọc cùng sử dụng vòng đeo tay thông minh để ghi lại số bước chân hai bạn đi mỗi ngày trong một tháng. Kết quả được ghi lại ở bảng sau:

a) Hãy tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Nếu so sánh theo độ lệch chuẩn thì bạn nào có số lượng bước chân đi mỗi ngày đều đặn hơn?
Giải rút gọn:
Cỡ mẫu: n = 30
Xét mẫu số liệu của Mai:
Số trung bình của mẫu số liệu là:
![]()
Phương sai của mẫu số liệu là:
![]()
Độ lệch chuẩn của mẫu số liệu là:
![]()
Xét mẫu số liệu của Ngọc:
Số trung bình của mẫu số liệu là:
![]()
Phương sai của mẫu số liệu là:
![]()
Độ lệch chuẩn của mẫu số liệu là:
![]()
b) Nếu so sánh theo độ lệch chuẩn thì bạn Ngọc có số lượng bước chân đi mỗi ngày đều đặn hơn.
GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA:
Giải rút gọn bài 1 trang 82 sách toán 12 tập 1 ctst: Bảng dưới đây thống kê cự ly ném tạ của một vận động viên.

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Giải rút gọn:
Ta có:
Giá trị đại diện | 19,25 | 19,75 | 20,25 | 20,75 | 21,25 |
Tần số | 13 | 45 | 24 | 12 | 6 |
Cỡ mẫu: n = 100
Số trung bình của mẫu số liệu ghép nhóm là:
![]()
Phương sai của mẫu số liệu ghép nhóm là:
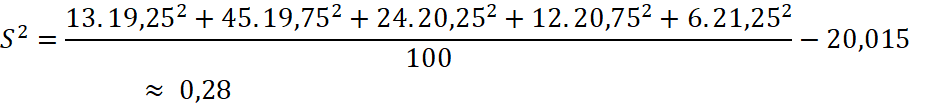
Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
![]()
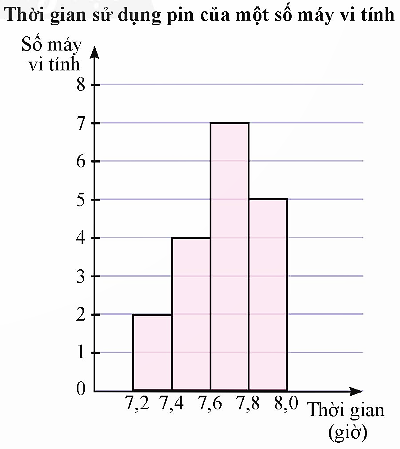
Giải rút gọn bài 2 trang 82 sách toán 12 tập 1 ctst: Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên.
a) Hãy cho biết có bao nhiêu máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ?
b) Hãy xác định số trung bình và độ lệch chuẩn của thời gian sử dụng pin.
Giải rút gọn:
a) Có hai máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ.
b) Ta có:
Giá trị đại diện | 7,3 | 7,5 | 7,7 | 7,9 |
Số máy | 2 | 4 | 7 | 5 |
Cỡ mẫu: n = 100
Số trung bình của thời gian sử dụng pin là:
![]()
Phương sai của thời gian sử dụng pin là:
![]()
Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
![]()
Giải rút gọn bài 3 trang 83 sách toán 12 tập 1 ctst: Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau:

a) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.
b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là ![]() và độ dài mỗi nhóm bằng 4.
và độ dài mỗi nhóm bằng 4.
c) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu.
Giải rút gọn:
a) Khoảng biến thiên của mẫu số liệu trên là: ![]() (km/h)
(km/h)
Cỡ mẫu: ![]()
Gọi ![]() là mẫu số liệu gốc về tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) và được xếp theo thứ tự không giảm.
là mẫu số liệu gốc về tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) và được xếp theo thứ tự không giảm.
Trung vị của mẫu số liệu là: ![]()
Tứ phân vị thứ nhất của mẫu số liệu là trung vị của nửa số liệu bên trái, do đó:
![]()
Tứ phân vị thứ ba của mẫu số liệu gốc là trung vị của nửa số liệu bên phải, do đó:
![]()
Vậy khoảng tứ phân vị của mẫu số liệu là:
![]()
Số trung bình của mẫu số liệu là:
![]()
Phương sai của mẫu số liệu là:
![]()
Vậy độ lệch chuẩn của mẫu số liệu là:
![]()
b)
Tốc độ | [42; 46) | [46; 50) | [50; 54) | [54; 58) | [58; 62) |
Số xe | 3 | 7 | 4 | 3 | 3 |
c) Cỡ mẫu n = 20.
Gọi ![]() là mẫu số liệu gốc gồm tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h)
là mẫu số liệu gốc gồm tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h)
Ta có ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
![]()
Giá trị đại diện | 44 | 48 | 52 | 56 | 60 |
Số xe | 3 | 7 | 4 | 3 | 3 |
Số trung bình của mẫu số liệu là:
![]()
Phương sai của mẫu số liệu là:
![]()
Vậy độ lệch chuẩn của mẫu số liệu là:
![]()
Giải rút gọn bài 4 trang 83 sách toán 12 tập 1 ctst: Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:

a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B.
b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
Giải rút gọn:
a)
| Giá trị đại diện | 31 | 33 | 35 | 37 | 39 |
| Số cây trồng ở địa điểm A | 25 | 38 | 20 | 10 | 7 |
| Số cây trồng ở địa điểm B | 22 | 27 | 19 | 18 | 14 |
Đường kính trung bình của thân cây xoan đào tại địa điểm A là:
![]()
Đường kính trung bình của thân cây xoan đào tại địa điểm B là:
![]()
Vậy đường kính trung bình của thân cây xoan đào trồng tại địa điểm B lớn hơn địa điểm A.
b) Độ lệch chuẩn của mẫu số liệu tại địa điểm A là:

Độ lệch chuẩn của mẫu số liệu tại địa điểm B là:

Vậy nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm A có đường kính đồng đều hơn.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải toán 12 Chân trời sáng tạo tập 1 bài 2 chương III, Giải bài 2 chương III toán 12 Chân trời sáng tạo tập 1, Siêu nhanh giải bài 2 chương III toán 12 Chân trời sáng tạo tập 1
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận