BÀI 3: ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

1. ĐƯỜNG TIỆM CẬN ĐỨNG

Hoạt động 1: Cho hàm số có đồ thị như Hình 1. 

a) Tìm ;  

b) Gọi là điểm trên đồ thị có hoành độ . Đường thẳng đi qua và vuông góc với trục cắt đường thẳng tại điểm . Tính theo và nhận xét về khi  và  . 

Giải rút gọn:

a) ;

b) Ta có:  

Khi và thì độ dài của MN càng giảm, điểm M di chuyển lại gần điểm N hơn. 

Thực hành 1: Tìm tiệm cận đứng của đồ thị của các hàm số sau: 

a) ;                      

b)

Giải rút gọn:

a) Tập xác định:

Ta có:

; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị . 

b) Tập xác định:

Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị . 

2. ĐƯỜNG TIỆM CẬN NGANG

Hoạt động 2: Cho hàm số có đồ thị như Hình 4. 

a) Tìm ;

b) Đường thẳng vuông góc với trục tại điểm cắt đồ thị hàm số tại điểm và cắt đường thẳng tại điểm (Hình 4). Tính theo và nhận xét về khi  và  .

Giải rút gọn:

a) ;

b) Ta có:  

Khi và  thì độ dài của MN càng giảm, điểm M di chuyển lại gần điểm N hơn. 

Thực hành 2: Tìm tiệm cận ngang của đồ thị của các hàm số sau: 

a) ;                       

b)

Giải rút gọn:

a) Tập xác định:

Ta có: ;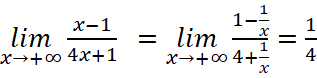  

Vậy đường thẳng là tiệm cận ngang của đồ thị hàm số.

b) Tập xác định:

Ta có:

Vậy đường thẳng là tiệm cận ngang của đồ thị hàm số.

3. ĐƯỜNG TIỆM CẬN XIÊN

Hoạt động 3: Cho đồ thị của hàm số và đường thẳng . Đường thẳng vuông góc với trục tại điểm cắt đồ thị hàm số tại điểm M và cắt đường thẳng tại điểm N (Hình 7). 

a) Tìm ;

b) Tính theo và nhận xét về khi  hoặc . 

Giải rút gọn:

a)                                     

b) Ta có:

Khi và  thì độ dài của MN càng giảm, điểm M di chuyển lại gần điểm N hơn. 

Thực hành 3: Tìm tiệm cận xiên của đồ thị hàm số .

Giải rút gọn:

Tập xác định:

Ta có:

Ta cũng có: ;

Đồ thị có tiệm cận xiên là đường thẳng

Thực hành 4: Nếu trong một ngày, một xưởng sản xuất được kilogam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: 

Tìm các đường tiệm cận của đồ thị hàm số

Giải rút gọn:

Tập xác định:

• Ta có: ; . 

Vậy đường thẳng hay trục tung là đường tiệm cận đứng của đồ thị 

• Ta có:

Vậy đường thẳng là tiệm cận ngang của đồ thị hàm số.

• Ta có:

Đồ thị không có tiệm cận xiên. 

Vậy đồ hàm số có đường thẳng hay trục tung là đường tiệm cận đứng và đường thẳng là tiệm cận ngang. 

4. GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA

Giải rút gọn bài 1 trang 24 sách toán 12 tập 1 ctst: Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau: 

a) ;                    

b)

c)

Giải rút gọn:

a) Tập xác định:

• Ta có: ; . 

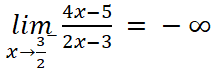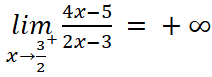Suy ra đường thẳng x = là đường tiệm cận đứng của đồ thị.

• Ta có:

Vậy đường thẳng y = 2  là tiệm cận ngang của đồ thị hàm số.

b) Tập xác định:

• Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:  

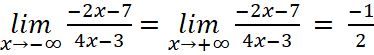
Vậy đường thẳng   là tiệm cận ngang của đồ thị hàm số.

c) Tập xác định:

• Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:  

Vậy đường thẳng   là tiệm cận ngang của đồ thị hàm số.

Giải rút gọn bài 2 trang 24 sách toán 12 tập 1 ctst: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:

a) ;                    

b) ;                       

c)

Giải rút gọn:

a) Tập xác định:

• Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:

Ta cũng có: ;

Đồ thị có tiệm cận xiên là đường thẳng

b) Tập xác định:

• Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:

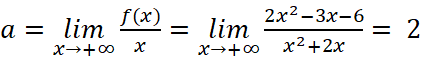
Ta cũng có: ;

Đồ thị có tiệm cận xiên là đường thẳng

c) Tập xác định:

• Ta có: ; . 

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:

Ta cũng có: ;

Đồ thị có tiệm cận xiên là đường thẳng

Giải rút gọn bài 3 trang 24 sách toán 12 tập 1 ctst: Tìm các tiệm cận của đồ thị hàm số sau:

Giải rút gọn:

a) Tập xác định:

• Ta có: ;

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có: ;

Suy ra đường thẳng là đường tiệm cận đứng của đồ thị.

• Ta có:  

Suy ra đường thẳng hay trục hoành là tiệm cận ngang của đồ thị hàm số.

b) Tập xác định:

• Ta có: ;

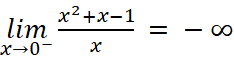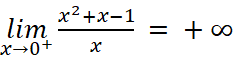
Suy ra đường thẳng hay trục tung là đường tiệm cận đứng của đồ thị.

• Ta có:

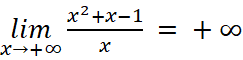
Vậy đồ thị không có đường tiệm cận ngang.

• Ta có:

Ta cũng có: ;

Đồ thị có tiệm cận xiên là đường thẳng

c) Tập xác định:

Đồ thị không có đường tiệm cận đứng. 

• Ta có:

Suy ra đường thẳng là tiệm cận ngang của đồ thị hàm số.

Giải rút gọn bài 4 trang 25 sách toán 12 tập 1 ctst: Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức với được tính theo và được tính theo giờ, . Tìm các đường tiệm cận của đồ thị hàm số . Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian trở nên rất lớn? 

Giải rút gọn:

Tập xác định:

Đồ thị không có đường tiệm cận đứng. 

Ta có:

Suy ra đường thẳng là đường tiệm cận ngang của đồ thị hàm số. 

Đồ thị không có đường tiệm cận xiên. 

Nhận xét: Nồng độ oxygen trong hồ sẽ gần đạt tới 5 khi thời gian trở nên rất lớn.

Giải rút gọn bài 5 trang 25 sách toán 12 tập 1 ctst: Tìm tiệm cận của đồ thị hàm số khối lượng hạt:

Giải rút gọn:

Tập xác định:

Ta có:

Vậy đường thẳng là tiệm cận đứng của đồ thị hàm số .