ĐẠI SỐ

Giải nhanh bài 1 trang 127 sgk toán 9 tập 2 kntt

Xét biểu thức với x 0.

a) Chứng minh rằng .

b) Tính giá trị biểu thức đã cho tại x = 64.

Giải nhanh:

a)

  (đpcm).

b)  

Giải nhanh bài 2 trang 127 sgk toán 9 tập 2 kntt

Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng AB = 36 000 km, tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí bên trên bề mặt Trái Đất. Cho biết bán kính Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị). 

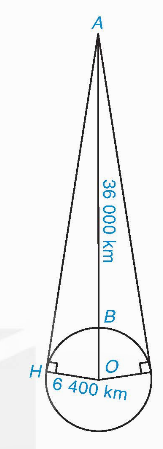
Giải nhanh:

Khoảng cách cần tìm là:

  (km).

Giải nhanh bài 3 trang 127 sgk toán 9 tập 2 kntt

Giải các bất phương trình sau:

a) –6x + 3(x + 1) > 4x – (x – 4);          b) (2x + 1)(2x – 1) < 4x² – 4x + 1.

Giải nhanh:

a) –6x + 3(x + 1) > 4x – (x – 4)

–3x + 3 > 3x + 4

–6x > 1 x < .

b) (2x + 1)(2x – 1) < 4x² – 4x + 1

4x² – 1 < 4x² – 4x + 1

4x < 5 x < .

Giải nhanh bài 4 trang 127 sgk toán 9 tập 2 kntt

Giải các phương trình sau:

a)            b)

Giải nhanh:

a)

  (thỏa mãn)

b)

  (thỏa mãn)

Giải nhanh bài 5 trang 127 sgk toán 9 tập 2 kntt

Kí hiệu (d₁) là đường thẳng x + 2y = 4, (d₂) là đường thẳng x – y = 1.

a) Vẽ (d₁) và (d₂) trên cùng một mặt phẳng tọa độ.

b) Giải hệ phương trình để tìm tọa độ giao điểm của hai đường thẳng (d₁) và (d₂).

Giải nhanh:

a) x – y = 1:

=> x = 0 thì y = –1

=> y = 0 thì x = 1

Đường thẳng đi qua điểm (0; –1) và (1; 0)

   x + 2y = 4:

=> x = 0 thì y = 2

=> y = 0 thì x = 4

Đường thẳng đi qua điểm (0; 2) và (4; 0)

b) Tọa độ giao điểm của hai đường thẳng (d₁) và (d₂) là:

Vậy tọa độ cần tìm là (1; 0).

Giải nhanh bài 6 trang 127 sgk toán 9 tập 2 kntt

Với mỗi giá trị đã cho của m, hãy giải hệ phương trình sau:

a)                       b)                   c)

Giải nhanh:

a)

Vậy hệ phương trình có nghiệm

 b  

(vô lí). 

Vậy hệ phương trình vô nghiệm.

c)  

Vậy là nghiệm của hệ phương trình.

Giải nhanh bài 7 trang 127 sgk toán 9 tập 2 kntt

Để chuẩn bị làm một ngôi nhà, chú Ba tính rằng tổng diện tích xây dụng là khoảng 100 m² và tổng chi phí (tiền vật liệu và tiền công thợ) hết khoảng 600 triệu đồng. Khi thực hiện diện tích xây dựng tăng thêm 20 m² và cứ mỗi mét vuông xây dựng, chi phí tiền vật liệu tăng thêm 10% và tiền công thợ tăng thêm so với dự tính ban đầu. Do đó tổng chi phí thực tế là 804 triệu đồng. Hỏi thực tế chú Ba phải trả bao nhiêu tiền vật liệu và bao nhiêu tiền công thợ cho mỗi mét vuông xây dựng?

Giải nhanh:

Số tiền nguyên liệu thực tế mỗi mét vuông xây dựng là x (x > 0, triệu đồng).

Số tiền công thợ thực tế mỗi mét vuông xây dựng là y (y > 0, triệu đồng).

=> Tiền nguyên liệu dự định là: 100x (triệu đồng).

=> Tiền công thợ dự định là: 100y (triệu đồng).

Diện tích thực tế là: 100 + 20 = 120 m².

Trên nguyên liệu cho 1 m² xây dựng thực tế là: x + 10%.x = 1,1x (triệu đồng).

=> Tiền nguyên liệu thực tế là: 120.1,1x = 132x (triệu đồng).

Tiền công thợ cho 1 m² xây dựng thực tế là: (triệu đồng).

=> Tiền công thợ thực tế là: 120.1,2y = 144y.

Ta có hệ phương trình:

  (thỏa mãn).

Vậy tiền nguyên liệu và tiền công thợ cho mỗi mét vuông xây dựng lần lượt là 5 triệu và 1 triệu.

Giải nhanh bài 8 trang 128 sgk toán 9 tập 2 kntt

Hai bến A và B trên một dòng sông cách nhau 36 km. Một ca nô xuôi dòng từ bến A đến bến B, rồi sau đó ngược dòng từ bến B về bến A hết thời gian bằng thời gian nó đi quãng đường 75 km khi nước yên lặng. Tính vận tốc thực của ca nô (tức là vận tốc của ca nô khi nước yên lặng), biết rằng vận tốc dòng nước là 3 km/h.

Giải nhanh:

Gọi vận tốc thực của ca nô là x (x > 3, km/h).

Vận tốc xuôi dòng là: x + 3 (km/h).

Vận tốc ngược dòng là: x – 3 (km/h).

Ca nô đi xuôi dòng là hết số thời gian là: (giờ).

Ca nô đi ngược dòng hết số thời gian là: (giờ).

Thời gian ca nô đi hết quãng đường 75 km khi nước yên lặng là: (giờ).

Ta có:

(vì x > 0). 

Vậy vận tốc thực của ca nô là 5 km/h.

HÌNH HỌC VÀ ĐO LƯỜNG

Giải nhanh bài 9 trang 128 sgk toán 9 tập 2 kntt

Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, HK = a (m), ngắm nhìn A với , ngắm nhìn B với góc .

a) Hãy biểu diễn AB theo a, , .

b) Khi a = 3 m, = 60^o, = 30^o, hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét). 

Giải nhanh:

a) - Xét tam giác AHK vuông tại H có:

- Xét tam giác BHK vuông tại H có:

- .

b) .

Giải nhanh bài 10 trang 128 sgk toán 9 tập 2 kntt

Cho tam giác ABC  vuông tại B có , AB = 6 cm. Vẽ tia Bt sao cho , cắt tia AC ở D (C nằm giữa A và D).

a) Chứng minh tam giác ABD cân tại B.

b) Tính khoảng cách từ D đến đường thẳng AB.

Giải nhanh:

a)

Xét tam giác ABD có:  

Tam giác ABD cân tại B.

b) Hạ DH BA tại H DH là khoảng cách cần tìm.

ABD cân tại B => BD = BA = 6 cm

.

Xét BHD vuông tại H có: 

(cm).

Giải nhanh bài 11 trang 128 sgk toán 9 tập 2 kntt

Tứ giác ABCD có hai góc đối diện B và D vuông góc, hai góc kia không vuông.

a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C).

b) Gọi I và K lần lượt là trung điểm các đường chéo AC và BD của tứ giác. Chứng minh rằng IK BD.

c) Kí hiệu các tiếp tuyến đường tròn (C) tại A, B và C lần lượt là a, b  và C. Giả sử b cắt a và c theo thứ tự E và F. Chứng minh rằng tứ giác AEFC là một hình thang.

d) Chứng minh rằng EF = AE + CF.

Giải nhanh:

a) - ABCD có hai góc đối diện và vuông => .

=> Tứ giác ABCD nội tiếp đường tròn.

=> có một đường tròn đi qua bốn điểm A, B, C và D

b) Xét đường tròn ngoại tiếp tứ giác ABCD có:

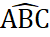• là góc nội tiếp chắn cung AC

• .

AC là đường kính đường tròn ngoại tiếp tứ giác ABCD.

Vì I là trung điểm AC (giả thiết) 

=> I là tâm đường tròn ngoại tiếp tứ giác ABCD.

IB = IC = R 

IBC cân tại I 

Tam giác IBC có IK là đường trung tuyến 

=> IK đồng thời là đường cao của tam giác IBC 

=> IK BD tại K.

c) - EA AC tại A, FC AC tại C

AEFC là hình thang.

d) - Xét đường tròn (I) có hai tiếp tuyến EA và EB cắt nhau tại E

EA = EB

Hai tiếp tuyến EF và CF cắt nhau tại F 

BF = FC 

=> EF = EB + BF = EA + FC 

Giải nhanh bài 12 trang 128 sgk toán 9 tập 2 kntt

Tỉ lệ các loại quả bán được trong một ngày của một của hàng được thể hiện trong biểu đồ hình quạt tròn như hình bên. Số phần trăm ghi trong mỗi hình quạt đúng bằng tỉ số giữa số đo của cung tròn tương ứng và số đo cảu cả đường tròn (360^o).

a) Tính số đo của mỗi cung tròn tương ứng với hình quạt màu tím, màu cam và màu đỏ.

b) Tính số đo của cung còn lại (ứng với hình quạt màu xanh) bằng hai cách. 

Giải nhanh:

a) Quạt màu tím: .

Quạt màu cam: .

Quạt màu đỏ: .

b) Số đo của cung tròn ứng với hình quạt màu xanh là: 

- Cách 1: .

- Cách 2: .

Giải nhanh bài 13 trang 129 sgk toán 9 tập 2 kntt

Cho tam giác ABC (AB < AC) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:

a) DBXF, DCYE  là các tứ giác nội tiếp.

b) Bốn điểm X, Y, E, F thẳng hàng.

Giải nhanh:

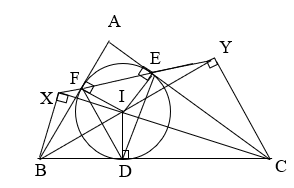
a) - Xét tứ giác BFID có: 

•  

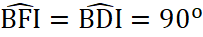
• Hai góc này ở vị trí đối diện nhau

Tứ giác BFID nội tiếp đường tròn đường kính BI (1).

- Xét tứ giác BXFI có:

• (giả thiết) 

• Hai góc này kề nhau, cùng nhìn xuống cạnh BI 

Tứ giác BXFI nội tiếp đường tròn đường kính BI (2).

Từ (1) và (2) 5 điểm B, F, I, D, F đều nằm trên đường tròn đường kính BI.

Tứ giác DBXF nội tiếp đường tròn đường kính BI.

Chứng minh tương tự: Tứ giác DCYE nội tiếp đường tròn đường kính IC.

b) - Ta có:

• (giả thiết)

• (giả thiết)

Mà  

.

Ta có: AE = AF 

Tam giác AEF cân tại A 

.

Có:

hay .

Y, E, F thẳng hàng (5).

Tương tự, X, E, F thẳng hàng (6).

Từ (5) và (6) Bốn điểm X, Y, E, F thẳng hàng.

Giải nhanh bài 14 trang 129 sgk toán 9 tập 2 kntt

Bạn Khôi làm một chiếc mũ sinh nhật bằng bìa cứng có dạng hình nón với đường kính đáy bằng 20 cm, độ dài đường sinh bằng 30 cm. Tính diện tích giấy để làm chiếc mũ sinh nhật trên ( lấy 3,14 và coi mép dán không đáng kể). 

Giải nhanh:

Chu vi đáy là: cm.

Số đo góc ở tâm là:

=> cm².

THỐNG KÊ VÀ XÁC SUẤT

Giải nhanh bài 15 trang 129 sgk toán 9 tập 2 kntt

Chiều cao (cm) của 20 bé trai 24 tháng tuổi được cho như bảng sau:

Theo Tổ chức Y tế thế giới WHO, nếu bé trai 24 tháng tuổi có chiều cao dưới 81,7 cm được coi là thấp còi, chiều cao từ 81,7 cm đến 93,9 cm được xem là đạt chuẩn, chiều cao từ 93,9 cm trở nên được xem là cao.

a) Hãy hoàn thiện bảng sau vào vở:

b) Tính tỉ lệ bé trai 24 tháng tuổi theo các mức phân loại về chiều cao. Vẽ biểu đồ hình quạt tròn biểu diễn các tỉ lệ thu được.

c) Ước lượng số bé trai thấp còi, đạt chuẩn, cao trong số 1 200 bé trai 24 tháng tuổi.

Giải nhanh:

a) 

b)

Tỉ lệ bé trai có chiều cao thấp còi là: .

Tỉ lệ bé trai có chiều cao đạt chuẩn là: .

Tỉ lệ bé trai có chiều cao cao là: .

c) Số bé trai có chiều cao thấp còi là: trẻ.

Số bé trai có chiều cao đạt chuẩn là: trẻ.

Số bé trai có chiều cao thấp còi là: trẻ.

Giải nhanh bài 16 trang 129 sgk toán 9 tập 2 kntt

Một nhóm của lớp 9A có 3 bạn nam và 2 bạn nữ. Giáo viên chọn ngẫu nhiên 2 bạn trong nhóm để tham gia một phong trào của trường.

a) Mô tả không gian mẫu.

b) Tính xác suất để hai bạn được chọn khác giới.

Giải nhanh:

a) = {(nam 1; nam 2), (nam 1; nam 3), (nam 2; nam 3), (nữ 1; nữ 2), (nữ 1; nam 1), (nữ 1; nam 2), (nữ 1; nam 3), (nữ 2; nam 1), (nữ 2; nam 2), (nữ 2; nam 3)}.

b) Có 6 kết quả  thuận lợi cho sự kiện hai bạn được chọn khác giới là (nữ 1; nam 1), (nữ 1; nam 2), (nữ 1; nam 3), (nữ 2; nam 1), (nữ 2; nam 2), (nữ 2; nam 3).

Xác suất để biến cố xảy ra là:

.