I. CÔNG THỨC CỘNG

LT-VD 1 trang 16 sgk toán 11 cánh diều

Tính sin...

Đáp án:

 $sin\frac{\pi}{12}=sin\frac{\pi}{3} cos\frac{\pi}{4}-cos\frac{\pi}{3} sin\frac{\pi}{4}$

= $\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}-\frac{1}{2}.\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$ 

LT-VD 2 trang 17 sgk toán 11 cánh diều

Tính $tan165^{\circ}$

Đáp án:

$cos 15^{\circ}=cos 45^{\circ}.cos 30^{\circ}+sin 45^{\circ}.sin 30^{\circ}$

= $\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}.\frac{1}{2}$

= $\frac{\sqrt{6}+\sqrt{2}}{4}$ 

LT-VD 3 trang 17 sgk toán 11 cánh diều

Tính $tan165^{\circ}$

Đáp án:

$tan 165^{\circ}= \frac{tan 120^{\circ}+tan 45^{\circ}}{1-tan 120^{\circ}tan 45^{\circ}}$

= $\frac{-\sqrt{3}+1}{1-(-\sqrt{3}).1}$

= $\frac{1-\sqrt{3}}{1+\sqrt{3}}$

= $-2+\sqrt{3}$ 

II. CÔNG THỨC NHÂN ĐÔI

LT-VD 4 trang 18 sgk toán 11 cánh diều

Cho... tính tan...

Đáp án:

$tan \alpha =\frac{2tan\frac{a}{2}}{1-\frac{a}{2}}=\frac{2.(-2)}{1-(-2)^{2}}=\frac{4}{3}$ 

LT-VD 5 trang 18 sgk toán 11 cánh diều

Tính: sin..., cos...

Đáp án:

+) $\frac{\pi}{8}=\frac{1-cos\frac{\pi}{4}}{2}=\frac{1-\frac{\sqrt{2}}{2}}{2}=\frac{2-\sqrt{2}}{2}$

Mà $sin\frac{\pi}{8}>0$ => $sin\frac{\pi}{8}=\frac{\sqrt{2-\sqrt{2}}}{2}$

+) $\frac{\pi}{8}=\frac{1+cos\frac{\pi}{4}}{2}=\frac{1+\frac{\sqrt{2}}{2}}{2}=\frac{2+\sqrt{2}}{2}$

Mà $cos\frac{\pi}{8}>0$ => $cos\frac{\pi}{8}=\frac{\sqrt{2+\sqrt{2}}}{2}$

III. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG

LT-VD 6 trang 19 sgk toán 11 cánh diều

Cho $cos a$... tính...

Đáp án:

$B=cos\frac{3a}{2} cos\frac{a}{2}$

= $\frac{1}{2}(cos 2a + cos a)$

$cos 2a = 2a-1=2.(\frac{2}{3})^{2}-1=-\frac{1}{9}$

=> $B=\frac{1}{2}.(-\frac{1}{9}+\frac{2}{3})=\frac{5}{18}$

IV. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH

LT-VD 7 trang 19 sgk toán 11 cánh diều

Tính...

Đáp án:

+) $sin\frac{7\pi}{9}+sin\frac{\pi}{9}=2sin\frac{4\pi}{9}cos\frac{\pi}{3}$

+) $cos\frac{7\pi}{9}-cos\frac{\pi}{9}=-2sin\frac{4\pi}{9}sin\frac{\pi}{3}$

=> $D=\frac{2sin\frac{4\pi}{9}cos\frac{\pi}{3}}{-2sin\frac{4\pi}{9}sin\frac{\pi}{3}}$

= $-cot\frac{\pi}{3}=-\frac{\sqrt{3}}{3}$

BÀI TẬP CUỐI SGK

BT 1 trang 20 sgk toán 11 cánh diều

Cho... tính...

Đáp án:

$cos\alpha= \frac{3}{5}$

=> $sin\alpha= \sqrt{1-(\frac{3}{5})^{2}}=\frac{4}{5}$ (do $sin\alpha>0$)

=> $tan\alpha=\frac{4}{3}$

$sin(\alpha+\frac{\pi}{6})=sin\alpha cos\frac{\pi}{6}+cos\alpha sin\frac{\pi}{6}=\frac{3+4\sqrt{3}}{10}$

$cos(\alpha-\frac{\pi}{3})=cos\alpha cos\frac{\pi}{3}+sin\alpha sin\frac{\pi}{3}=\frac{3+4\sqrt{3}}{10}$

$tan(\alpha+\frac{\pi}{4})=\frac{tan\alpha+tan\frac{\pi}{4}}{1-tan\alpha.tan\frac{\pi}{4}}=-7$

BT 2 trang 20 sgk toán 11 cánh diều

Tính...

Đáp án:

$A=sin(a-17^{\circ}-a-13^{\circ})=sin(-30^{\circ})=-\frac{1}{2}$

$B=cos(b+\frac{\pi}{3}+\frac{\pi}{6}-b)=cos\frac{\pi}{2}=0$

BT 3 trang 20 sgk toán 11 cánh diều

Cho $tan(a+b) = 3$, $tan(a−b) = 2$. Tính: $tan 2a$, $tan 2b$.

Đáp án:

$tan2a=\frac{tan(a+b)+tan(a-b)}{1-(a-b)tan(a-b)}=\frac{3+2}{1-3.2}=-1$

$tan2b=\frac{tan(a+b)-tan(a-b)}{1+(a-b)tan(a-b)}=\frac{3-2}{1+3.2}=\frac{1}{7}$

BT 4 trang 20 sgk toán 11 cánh diều

Cho $sin a =$... Tính: $cos 2a$, $cos 4a$.

Đáp án:

$cos 2a =1-2a =-\frac{3}{5}$ 

$cos 4a =22a-1=-\frac{7}{25}$

BT 5 trang 20 sgk toán 11 cánh diều

Cho $sin a + cos a = 1$. Tính: $sin 2a$.

Đáp án:

$sin a +cos a =1$⟺ $(sin a +cos a)^{2}=1$

⟺ $a +a +2.sin a .cos a =1$ 

⟺ $2a =1$

⟺ $sin 2a =0$

BT 6 trang 21 sgk toán 11 cánh diều

Cho $cos 2a$=... tính $sin a$, $cos a$, $tan a$.

Đáp án:

$a=\frac{1-cos2a}{2}=\frac{1-\frac{1}{3}}{2}=\frac{1}{3}$

=> $sin a=\frac{\sqrt{3}}{3}$ (do sin a >0)

$a=\frac{1+cos2a}{2}=\frac{1+\frac{1}{3}}{2}=\frac{2}{3}$

=> $cos a=\frac{-\sqrt{6}}{3}$ (do cos a <0)

$tan a=\frac{\frac{\sqrt{3}}{3}}{-\frac{\sqrt{6}}{3}}=\frac{-\sqrt{2}}{2}$

BT 7 trang 22 sgk toán 11 cánh diều

Cho $cos 2x =$... tính...

Đáp án:

$A=\frac{1}{2}[cos2x+cos\frac{\pi}{3}]=\frac{3}{8}$

$B=\frac{-1}{2}[cos2x-cos\frac{2\pi}{3}]=\frac{-3}{8}$

BT 8 trang 23 sgk toán 11 cánh diều

Rút gọn biểu thức: A...

Đáp án:

$A=\frac{2sin x.cos x}{1+(x-1)}=\frac{2sin x.cos x}{x}=\frac{sin x}{cos x}=tan x$

BT 9 trang 24 sgk toán 11 cánh diều

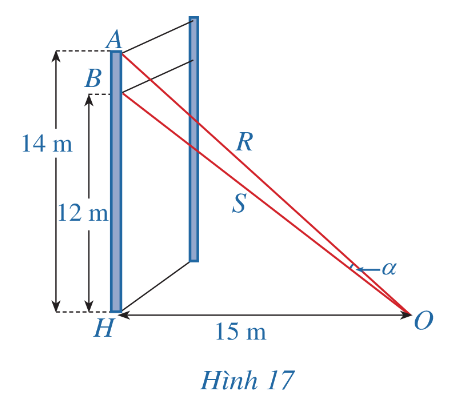
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m.

a) Tính $tan \alpha $ ở đó α là góc giữa hai sợi cáp trên.

b) Tìm góc $\alpha$ (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Đáp án:

a) 

+) Xét ∆AOH : $tan \widehat{AOH}=\frac{AH}{HO}=\frac{14}{15}$

+) Xét ∆BOH: $tan \widehat{BOH}=\frac{BH}{HO}=\frac{12}{15}=\frac{4}{5}$

=> $tan =tan (\widehat{AOH}-\widehat{BOH})$

= $\frac{\frac{14}{15}-\frac{4}{5}}{1+\frac{14}{15}.\frac{4}{5}}$

= $\frac{\frac{2}{15}}{\frac{131}{75}}=\frac{10}{131}$

b) 

   $ \alpha \approx 4^{\circ}$

BT 10 trang 25 sgk toán 11 cánh diều

Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Đáp án:

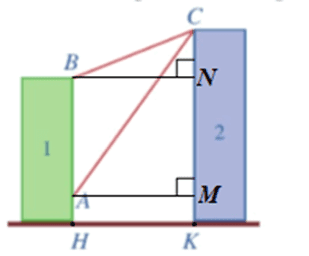
Kẻ BN⊥CK và AM⊥CK

$MK = AH = 6$   

$MN = AB = 24 – 6 = 18$

$CN = 32 – 6 – 18 = 8  $  

$HK = AM = BN = 20$ 

$CM = 32 – 6 = 26$

+) $\triangle AMC$ có $tan\widehat{ACM}=\frac{AM}{CM}=\frac{20}{26}=\frac{10}{13}$

+) $\triangle BNC$ có $tan\widehat{BCN}=\frac{BN}{CN}=\frac{20}{8}=\frac{5}{2}$

=> $tan\widehat{ACB}=tan(\widehat{BCN}-\widehat{ACM})=\frac{\frac{5}{2}-\frac{10}{13}}{1+\frac{5}{2}.\frac{10}{13}}=\frac{45}{76}$

=> $\widehat{ACB} \approx 30,63^{\circ}$