I. ĐỊNH NGHĨA

LT-VD 1 trang 53 sgk toán 11 cánh diều

Cho cấp số nhân ($u_{n}$) với $u_{1}$ = −6, $u_{2}$ = −2. 

a) Tìm công bội q

b) Viết năm số hạng đầu của cấp số nhân đó

Đáp án:

a)  q = (-2) : ( -6) = $\frac{1}{3}$

b) $u_{1}$=-6; $u_{2}$=-2; $u_{3}=-\frac{2}{3}$ ; $u_{4}=-\frac{2}{9}$; $u_{5}=-\frac{2}{27}$.

LT-VD 2 trang 54 sgk toán 11 cánh diều

Cho dãy số ($u_{n}$) với $u_{n}=3.2^{n}$ ($n\geq$ 1). Dãy ($u_{n}$) có là cấp số nhân không? Vì sao?

Đáp án:

$\frac{u_{n+1}}{u_{n}}=\frac{3.2^{n+1}}{3.2^{n}}=2$ với $n\geq$ 1 => dãy ($u_{n}$) là cấp số nhân.

II. SỐ HẠNG TỔNG QUÁT

LT-VD 3 trang 55 sgk toán 11 cánh diều

Bác Linh gửi vào ngân hàng 100 triệu đồng tiền tiết kiệm với hình thức lãi kép, kì hạn 1 năm với lãi suất 6%/năm. Viết công thức tính số tiền (cả gốc và lãi) mà bác Linh có được sau n năm (giả sử lãi suất không thay đổi qua các năm)

Đáp án:

Sau n năm bác Linh có số tiền là :  $T_{n+1}$=100.(1+6%) $^{n}$ (triệu đồng)

III. TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ NHÂN

LT-VD 4 trang 55 sgk toán 11 cánh diều

Tính tổng n số hạng đầu của mỗi cấp số nhân sau:

a) 3,−6,12,−24,... với n = 12

b) 1/10, 1/100, 1/1000 với n = 5

Đáp án:

a) $S_{12}=\frac{3[1-(-2)^{12}]}{1-(-2)}=-4095$ 

b) $S_{5}=\frac{\frac{1}{10}[1-(\frac{1}{10})^{5}]}{1- \frac{1}{10}}=0,11111$

BÀI TẬP CUỐI SGK

BT 1 trang 56 sgk toán 11 cánh diều

Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) 5; −0,5; 0,05; −0,005; 0,0005

b) −9, 3, −1, 1/3, −1/9

c) 2, 8, 32, 64, 256

Đáp án:

a) Công bội $q = -\frac{1}{10}$ => dãy số là cấp số nhân

b) Công bội $q=-\frac{1}{3}$ => dãy số là cấp số nhân

c) $\frac{8}{2}=\frac{32}{8} \neq \frac{64}{32}$ => dãy số không là cấp số nhân

BT 2 trang 56 sgk toán 11 cánh diều

Chứng minh mỗi dãy số ($u_{n}$) với số hạng tổng quát như sau là cấp số nhân...

Đáp án:

a) $q=(-\frac{3}{4}.2^{n+1}):(-\frac{3}{4}.2^{n})=2$

b) $q=\frac{5}{3^{n+1}}:\frac{5}{3^{n}}=\frac{1}{3}$ 

c) $q=(-0,75)^{n+1}:(-0,75)^{n}=-0,75$

BT 3 trang 56 sgk toán 11 cánh diều

Cho cấp số nhân ($u_{n}$) với số hạng đầu $u_{n}$ = −5, công bội q = 2. 

a) Tìm $u_{9}$. 

b) Số −320 là số hạng thứ bao nhiêu của cấp số nhân trên?

c) Số 160 có phải là một số hạng của cấp số nhân trên không?

Đáp án:

a) $u_{9}=(-5).2^{9-1}=-1280$

b) $(-5).2^{n-1}$=-320 ⬄ n =7 => Số -320 là số hạng thứ 7.

c) $(-5).2^{n-1}$=160  ⬄ n = -4∉N* => số 160 không là số hạng của dãy số.

BT 4 trang 56 sgk toán 11 cánh diều

Cho cấp số nhân ($u_{n}$) với $u_{1}$ = 3, $u_{3}$ = 27/4

a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên

b) Tính tổng 10 số hạng đầu của cấp số nhân trên

Đáp án:

a) $u_{3}=u_{1}.q^{2}$ ⬄ $q^{2} = \frac{27}{4} : 3 = \frac{9}{4}$ 

⬄ q = ± $\frac{3}{2}$

+)  $q=\frac{3}{2}$

=> 5 số hạng đầu của cấp số nhân là:  $3; \frac{9}{4} ; \frac{27}{4} ; \frac{81}{8} ; \frac{243}{16}$

+)  $q=-\frac{3}{2}$ 

=> 5 số hạng đầu của cấp số nhân là:  $3; -\frac{9}{4} ; \frac{27}{4} ; -\frac{8}{18} ; \frac{243}{16}$

b) +) $q = \frac{3}{2}$     

=> $S_{10}=\frac{3.(1-(\frac{3}{2})^{10}}{1-\frac{3}{2}}$ ≈340 

+) $q =-\frac{3}{2}$ 

=> $S_{10}=\frac{3.(1-(-\frac{3}{2})^{10}}{1-(-\frac{3}{2}}$ ≈-68

BT 5 trang 56 sgk toán 11 cánh diều

Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi $u_{n}$ là dân số của tỉnh đó sau n năm. Giả sử tỉ lệ tăng dân số là không đổi

a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020

b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020

Đáp án:

a) $u_{n}$=2.(1+1%) $^{n-1}$ (triệu dân).

b) $u_{10}$=2.(1+1%) $^{10-1}$ ≈2,19 (triệu dân).

BT 6 trang 56 sgk toán 11 cánh diều

Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó). 

a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng. 

b) Viết công thức tính giá trị của ô tô sau n năm sử dụng. 

c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Đáp án:

a) $u_{1}$=800-800.4%=800.(1-4%)=768 (triệu đồng)

$u_{2}$=800.(1-4%) $^{2}$ =737,28 (triệu đồng)

b) $u_{n}$=800.(1-4%) $^{n}$.

c) $u_{10}$=800.(1-4%) $^{10}$ ≈531,87 (triệu đồng).

BT 7 trang 56 sgk toán 11 cánh diều

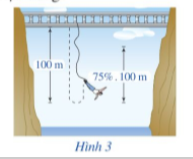
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100 m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống.

Đáp án:

Tổng quãng đường người chơi rơi xuống sau 10 lần là : 

$100.(\frac{1-0,75^{10}}{1-0,75})$ (m)

Tổng quãng đường người chơi được kéo lên sau 10 lần là : 

$75. (\frac{1-0,75^{10}}{1-0,75})$ (m)

Tổng quãng đường người đó đi được sau 10 lần rơi xuống và được kéo lên là :

$175.(\frac{1-0,75^{10}}{1-0,75})$ ≈661m