BÀI 1. HÀM SỐ VÀ ĐỒ THỊ

I. HÀM SỐ

Bài 1: Trong y học, một người cân nặng 60kg chạy với tốc độ 6,5k km/h thì lượng calo tiêu thụ được tính theo công thức: c=4,7t (Nguồn: https://irace.vn), trong đó thời gian t được tính theo phút. Hỏi c có phải là hàm số của t không? Vì sao?

Đáp án chuẩn:

c là hàm số của t vì mỗi giá trị của t chỉ cho đúng một giá trị của c

Bài 2: Tìm tập xác định của hàm số:

Đáp án chuẩn:

D = [-2;+)\{3}

Bài 3: Cho hàm số:

a. Tìm tập xác định của hàm số trên.

b. Tính giá trị của hàm số khi x=−1; x=2022

Đáp án chuẩn:

a.

b. x = -1   y = 1; x = 2022 y = 2022

II. ĐỒ THỊ CỦA HÀM SỐ 

Bài 1: Cho hàm số y = và ba điểm M(−1;−1),N(0;2),P(2;1). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?

Đáp án chuẩn:

N; P

Bài 2: Dựa vào Hình 4, xác định g(−2),g(0),g(2)

Đáp án chuẩn:

+ g(-2) = -1

+ g(0) = 0

+ g( 2) = -1

III. SỰ BIẾN THIÊN CỦA HÀM SỐ 

Bài 1: Chứng tỏ hàm số y=6x² nghịch biến trên khoảng (−∞;0)

Đáp án chuẩn:

Xét hai số bất kì x₁, x₂ ( sao cho x₁ < x₂

Do x₁ < x₂ < 0 nên f(x₁) > f(x₂) => đpcm

BÀI TẬP CUỐI SGK

Bài tập 1: Tìm tập xác định của mỗi hàm số sau:

a) y = -x² 

b)

c) y =

d) y = {1 nếu x ∈ Q; 0 nếu x ∈ R∖Q. 

Đáp án chuẩn:

a. D =

b. D = (-

c. D = \{-1}

c. D =

Bài tập 2: Bảng dưới đây cho biết chỉ số PM2,5 (bụi mịn) ở Thành phố Hà Nội từ tháng 1 đến tháng 12 của năm 2019.

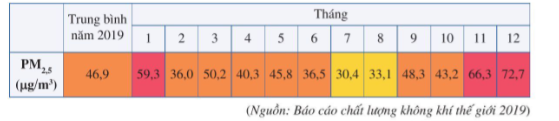
a. Nêu chỉ số PM2,5 trong tháng 2; tháng 5, tháng 10.

b. Chỉ số PM2,5 có phải là hàm số của tháng không? Tại sao?

c. Bụi mịn PM2,5 có đường kính nhỏ hơn 2,5 μm (mi-crô-mét) dễ dàng xâm nhập vào cơ thể con người thông qua đường hô hấp và gây nên một số bệnh nguy hiểm như đột quỵ, tim mạch... Em hãy nêu một số biện pháp bảo vệ bản thân trước bụi mịn.

Đáp án chuẩn:

a. Tháng 2 là 36,0 μg/m3 ; trong tháng 5 là 45,8 μg/m3; trong tháng 10 là 43,2 μg/m3.

b. PM_2,5 là hàm số của tháng

c) HS tự trả lời

Bài tập 3: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250g như trong bảng sau:

a. Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x (g) hay không? Nếu đúng, hãy xác định những công thức tính y.

b. Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g (không kể phụ phí và thuế VAT).

Đáp án chuẩn:

a.

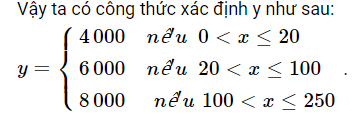
b. x = 150 y = 8000; x = 2000 y = 8000

Bài tập 4: Cho hàm số y=−2x²

a. Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng - 2; 3 và 10.

b. Tìm những điểm thuộc đồ thị hàm số có tung độ bằng - 18.

Đáp án chuẩn:

a. (-2;-8); (3;-18); (10;-200)

b.  (3;-18); (-3;-18) 

Bài tập 5:  Cho đồ thị hàm số y=f(x) như Hình 8.

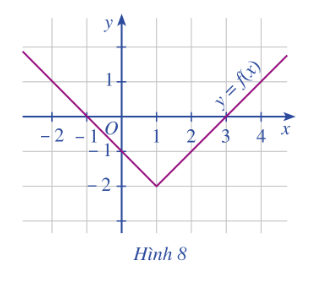
a. Trong các điểm có toạ độ (1;−2), (0;0), (2;−1), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?

b. Xác định f(0); f(3).

c. Tìm điểm thuộc đồ thị có tung độ bằng 0.

Đáp án chuẩn:

a. Điểm (1;-2); (2;-1) thuộc đồ thị hàm số, điểm (0;0) không thuộc đồ thị hàm số. 

b. f(0) = -1; f(3) = 0 

c. (3;0) hoặc (-1;0)

Bài tập 6:  Cho hàm số y = . Chứng tỏ hàm số đã cho:

a. Nghịch biến trên khoảng (0;+∞)

b. Nghịch biến trên khoảng (−∞;0)

Đáp án chuẩn:

a. Xét hai số bất kì x₁, x₂ (0;+) sao cho 0 < x₁ < x₂

Ta có: 0 < x₁ < x₂ nên f(x₁) > f(x₂) => đpcm

b. Xét hai số bất kì x₁, x₂ (-;0) sao cho x₁ < x₂ <0

Ta có: x₁ < x₂ < 0 nên f(x₁) f(x₂) => đpcm

Bài tập 7: Cho hàm số y=f(x) có đồ thị như Hình 9.

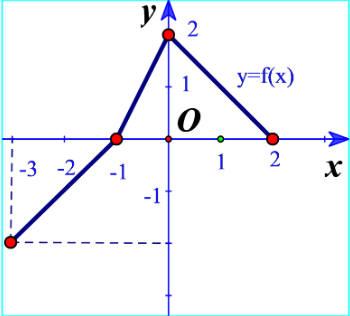
Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số 

y=f(x).

Đáp án chuẩn:

Hàm số đồng biến trên khoảng (−3;0) và nghịch biến trên khoảng (0;2)

Bài tập 8: Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá. Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe. Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất?

Đáp án chuẩn:

Nên chọn công ty A để chi phí là thấp nhất.