I. HÀM SỐ 

Định nghĩa

HĐ1:

a. Thay t = 1 vào S ta được:

$S = \frac{1}{2} . 9,8 . 1^2 = 4,9 (m)$

Thay t = 2 vào S ta được:

b. $S = \frac{1}{2}.9,8.2^2 = 19,6 (m)$

Với mỗi giá trị của t có 1 giá trị tương ứng của S. 

HĐ2:

a. Ta có: $y = - 200x^2 + 92 000x – 8 400 000$ (1)

Thay x = 100 vào (1) ta được: 

$y = -200.200^2 + 92 000.100 – 8 400 000 = -1 200 000$

Thay x = 200 vào (1) ta được: 

$y = -200.200^2 + 92 000.200 – 8 400 000 = 2 000 000$

Với mỗi giá trị của x, có một giá trị tương ứng của y 

Kết luận: 

Cho tập hợp rỗng D ⊂ R. Nếu với mỗi giá trị của x thuộc D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực R thì ta có một hàm số. 

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số. 

Kí hiệu hàm số: y = f(x), x∈D

Ví dụ 1 (SGK – tr32)

Luyện tập 1: 

c là hàm số của t vì mỗi giá trị của t chỉ cho đúng một giá trị của c.

2. Cách cho hàm số

Hàm số cho bằng một công thức

HĐ3:

a. Biểu thức xác định của hàm số (1) và (2) lần lượt là $2x + 1$ và $\sqrt{x-2}$

b. Biểu thức $2x + 1$ có nghĩa với mọi x ∈ R

c. Biểu thức $\sqrt{x-2}$ có nghĩa khi $x – 2 \geq 0 \leftrightarrow x \geq 2$.

Kết luận:

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. 

Ví dụ 2 (SGK – tr32)

Luyện tập 2: 

Biểu thức $y= \frac{\sqrt{x+2}}{x-3}# có nghĩa khi

${\left\{\begin{matrix}
x+2\geq 0 & & \\
x-3\neq 0& &
\end{matrix}\right.}
\rightarrow \left\{\begin{matrix}
x \geq-2 & & \\
x \neq 3 & &
\end{matrix}\right.$

Vậy tập xác định của hàm số đã cho là D = [-2;+)\{3}

Hàm số cho bằng nhiều công thức

Ví dụ 3 (SGK – tr33)

Chú ý: 

Cho hàm số y = f(x) với tập xác định là D. Khi biến số x thay đổi trong tập D thì tập hợp các giá trị y tương ứng được gọi là tập giá trị của hàm số đã cho.

Luyện tập 3:

a. D=R\0

b. x = -1 < 0 y = -x = 1

c. x = 2022 > 0 $\leftrightarrow$ y = x = 2022

Hàm số không cho bằng công thức 

Ví dụ 4 (SGK – tr33)

II. ĐỒ THỊ CỦA HÀM SỐ

HĐ4:

a. Thay $x_1 = -1; x_2 = 1$ vào $y_1 = f(x_1), y_2 = f(x_2)$ ta được:

$y_1 = f(-1) = (-1)^2; y_2 = f(1) = 1^2 = 1$

Ta có $x_1 = -1; y_1 = 1 =>  M_1 (-1;1)$; 

$x_2 = 1; y_2 = 1 =>  M_2(1;1)$

Biểu diễn các điểm trên mặt phẳng:

Kết luận: 

Đồ thị của hàm số y = f(x) xác định trên tập hợp D là tập hợp tất cả các điểm M(x;f(x)) trong mặt phẳng toạ độ Oxy với mọi x thuộc D. 

Ví dụ 5 (SGK – tr34)

Nhận xét:

+ Điểm M(a;b) trong mặt phẳng toạ độ thuộc đồ thị hàm số y = f(x), x D khi và chỉ khi

${\left\{\begin{matrix}
a\in D& & \\
b=f(a)& &
\end{matrix}\right.}$

+ Để chứng tỏ điểm M(a;b) trong mặt phẳng toạ độ không thuộc đồ thị hàm số $y = f(x), x \in D$, ta có thể kiểm tra một trong hai khả năng sau:

Khả năng 1: Chứng tỏ rằng $a \in D$

Khả năng 2: Khi a ∈ D thì chứng tỏ rằng $b \neq f(a)$.

Luyện tập 4:

$y = \frac{1}{x}$   (1)

Tập xác định: D = R\{0}

Điểm N (0;2) có x = 0 Điểm N không thuộc đồ thị 

Điểm M (-1;-1) có x = -1 thay vào (1) ta được: $y = \frac{1}{-1} = -1$ =>  Điểm M thuộc đồ thị 

Điểm P (2;1) có x = 2 thay vào (1) ta được $y =\frac{1}{2}$≠1  Điểm P không thuộc đồ thị.

Ví dụ 6 (SGK – tr35)

III. SỰ BIẾN THIÊN CỦA HÀM SỐ

HĐ5:

Ta có: f(1) = 1 + 1 = 2; f(2) = 2 + 1 = 3. Vậy f(1) < f(2)

Ta có: $f(x_1) = x_1 + 1; f(x_2) = x_2 + 1$

Vì $x_1 < x_2$ nên $x_1 + 1 < x_2 + 1$ liên hệ giữa thứ tự và phép cộng. 

Vậy $f(x_1) < f(x_2)$ với mọi $x_1, x_2$ ∈ R.

Ví dụ 8 (SGK – tr36)

Luyện tập 6:

Xét hai số bất kì $x_1, x_2 \neq (-∞;0)$ sao cho $x_1 < x_2$. 

Do $x_1 < x_2 < 0$ nên $6x_1^2 > 6x_2^2$ hay $f(x_1) > f(x_2)$

Vậy hàm số nghịch biến trên khoảng (-∞;0).

Nhận xét: 

Xét sự biến thiên của một hàm số là tìm các khoảng hàm số đồng biến và các khoảng hàm số nghịch biến. Kết quả xét sự biến thiên được tổng kết trong một bảng biến thiên.   

Chẳng hạn, sau đây là bảng biến thiên của hàm số $y = 6x^2$ 

+ Dấu mũi tên đi xuống (từ + đến 0) diễn tả hàm số nghịch biến trên khoảng (-∞;0)

+ Dấu mũi tên đi lên (từ 0 đến + ) diễn tả hàm số đồng biến trên khoảng (0; + ). 

Mô tả hàm số đồng biến, hàm số nghịch biến bằng đồ thị. 

HĐ6: 

Quan sát đồ thị hàm số ta thấy: f(-2) = 4, f(-1) = 1. Vì 4 > 1 nên f(-2) > f(-1).

=> Hàm số nghịch biến trên (-2;-1) 

Vậy giá trị của hàm số giảm khi x tăng từ -2 đến -1.  

Quan sát đồ thị hàm số ta thấy: f(1) = 1; f(2) = 4. Vì 4 > 1 nên f(2) > f(1). 

Hàm số đồng biến trên (1;2)

Vậy giá trị của hàm số tăng khi x tăng từ 1 đến 2. 

Nhận xét: 

+ Hàm số đồng biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số “đi lên” trên khoảng đó. 

+ Hàm số nghịch biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số “đi xuống” trên khoảng đó. 

Khi nói đồ thị “đi lên” hay “đi xuống”, ta luôn kể theo chiều tăng của biến số, nghĩa là kể từ trái qua phải. 

Ví dụ 9 (SGK – tr37)

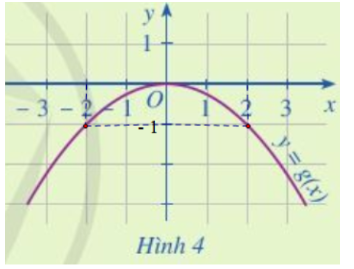
Luyện tập 5:

+ g(-2) = -1.

+ g(0) = 0.

+ g( 2) = -1.