BÀI 5. TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ

I. ĐỊNH NGHĨA

Bài 1: Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G. Tìm các số a, b biết: 

;

Đáp án chuẩn:

a = ; b =

II. TÍNH CHẤT

Bài 1: Cho ba điểm A,B,C. Chứng minh

Đáp án chuẩn:

III. MỘT SỐ ỨNG DỤNG

Bài 1: Cho tam giác ABC có G là trọng tâm. Chứng minh 3

Đáp án chuẩn:

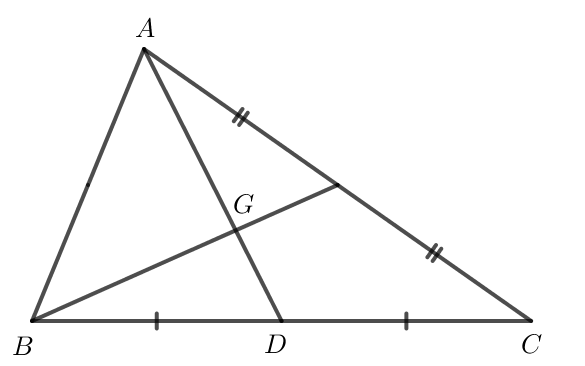
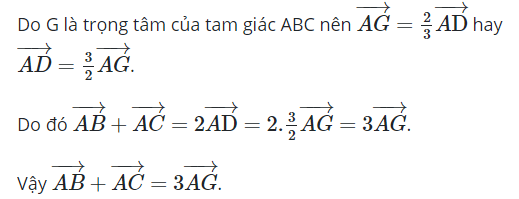
Bài 2: Ở Hình 61, tìm k trong mối trường hợp sau:

a.

b.

Đáp án chuẩn:

a.

b.

BÀI TẬP CUỐI SGK

Bài tập 1: Cho hình thang MNPQ, MN//PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?

A.

B.

C.

D.

Đáp án chuẩn:

C

Bài tập 2: Cho đoạn thẳng AB=6 cm

a. Xác định điểm C thỏa mãn AC

b. Xác định điểm D thỏa mãn AD 

Đáp án chuẩn:

a. A, B, C thẳng hàng, C là trung điểm của AB và AC = 3cm

b. D, A, B thẳng hàng, D thuộc tia đối của tia AB sao cho AD = 3 cm

Bài tập 3: Cho tam giác ABC có M,N,P lần lượt là trung điểm của BC, CA, AB. Chứng minh:

a.  

b.

Đáp án chuẩn:

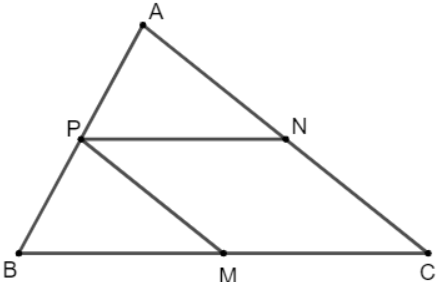
a.

b.

Bài tập 4: Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE =EC (Hình 62). Giả sử ; . Biểu diễn các vectơ theo

Đáp án chuẩn:

Bài tập 5: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm tam giác BCD. Chứng minh:

a.

b.

c. G thuộc đoạn thẳng AE và

Đáp án chuẩn:

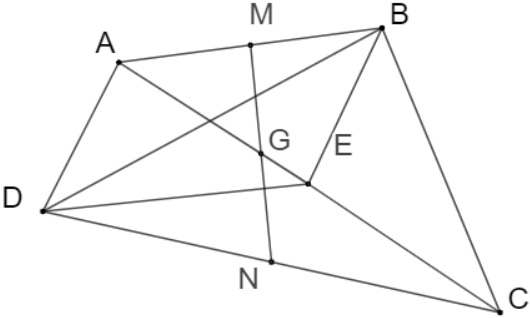
a.

b. (đpcm)

c. Vì EA = 4 EG nên AG =3434 AE.

Bài tập 6: Cho hình bình hành ABCD. Đặt ; . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vecto  

Đáp án chuẩn:

;

Bài tập 7: Cho tam giác ABC. Các điểm D, E, H thỏa mãn ;

 ;

a. Biểu thị mỗi vectơ theo hai vectơ

b. Chứng minh D, E, H thẳng hàng

Đáp án chuẩn:

a.

b. Chứng minh 

Vậy D, E, H thẳng hàng