A. PHƯƠNG PHÁP GIẢI

1. Tỉ số lượng giác của góc nhọn

Cho góc nhọn $\alpha $, từ một điểm bất kì trên một cạnh của góc $\alpha $, kẻ đường vuông góc với cạnh kia:

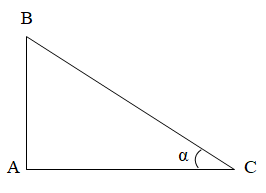
Khi đó:

• sin$\alpha $ = $\frac{Cạnh đối}{Cạnh huyền}=\frac{AB}{BC}$
• cos$\alpha $ = $\frac{Cạnh kề}{Cạnh huyền}=\frac{AC}{BC}$
• tan$\alpha $ = $\frac{Cạnh đối}{Cạnh kề}=\frac{AB}{AC}$
• cot$\alpha $ = $\frac{Cạnh kề}{Cạnh đối}=\frac{AC}{AB}$

Nhận xét: Vì độ dài của các cạnh trong một tam giác vuông đều dương và hai cạnh góc vuông nhỏ hơn cạnh huyền nên 0 < sin$\alpha $ < 1, 0 < cos$\alpha $ < 1; tan$\alpha $ > 0; cot$\alpha $ > 0.

2. Tỉ số lượng giác của hai góc phụ nhau

• Tỉ số lượng giác của hai góc phụ nhau (có tổng số đo bằng $90^{0}$) thì: sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Trên hình: sinB = cosC; cosB = sinC

                 tanB = cotC; cotB = tanC

Ví dụ 1: Cho tam giác ABC vuông tại C, có BC = 1,2; CA = 0,9. Tính cá tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.

Hướng dẫn:

Áp dụng hệ thức Py-ta-go vào tam giác ABC vuông tại C, ta có:

$AB^{2}=BC^{2}+CA^{2}=1,2^{2}+0,9^{2}=1,5^{2}$ => AB = 1,5

Ta có:

• tanB = $\frac{CA}{CB}$ = $\frac{0,9}{1,2}$ = $\frac{3}{4}$
• cotB = $\frac{CB}{CA}$ = $\frac{1,2}{0,9}$ = $\frac{4}{3}$
• sinB = $\frac{CA}{AB}$ = $\frac{0,9}{1,5}$ = $\frac{3}{5}$
• cosB = $\frac{CB}{AB}$ = $\frac{1,2}{1,5}$ = $\frac{4}{5}$

Vì góc A và góc B phụ nhau, nên:

• cotA = tanB = $\frac{3}{4}$
• tanA = cotB = $\frac{4}{3}$
• sinA = cosB = $\frac{4}{5}$
• cosA = sinB = $\frac{0,9}{1,5}$ = $\frac{3}{5}$

3. Một số hệ thức cơ bản

• $tan\alpha =\frac{sin\alpha }{cos\alpha }$         
• $cot\alpha =\frac{cos\alpha }{sin\alpha }$
• $tan\alpha .cot\alpha =1$                                 
• $sin^{2}\alpha +cos^{2}\alpha =1$
• $tan^{2}\alpha +1=\frac{1}{cos^{2}\alpha }$     
• $cot^{2}\alpha +1=\frac{1}{sin^{2}\alpha }$

4. So sánh các tỉ số lượng giác 

Cho $\alpha ;\beta $ là hai góc nhọn. Nếu $\alpha <\beta $ thì

• sin$\alpha $ < sin$\beta $; tan$\alpha $ < tan$\beta $
• cos$\alpha $ < cos$\beta $; cot$\alpha $ < cot$\beta $

Ví dụ 2: Không dùng bẳng số máy tính hãy so sánh:

a, sin20$^{0}$ và sin70$^{0}$                    b, cos25$^{0}$ và cos63$^{0}$15'

c, tan73$^{0}$20' và tan45$^{0}$              d, cot20$^{0}$ và cot37$^{0}$40'

Hướng dẫn:

a, Vì 20$^{0}$ < 70$^{0}$ nên sin20$^{0}$ < sin70$^{0}$    

b, Vì 25$^{0}$ < 63$^{0}$15' nên cos25$^{0}$ > cos63$^{0}$15'

c, Vì 73$^{0}$20' < 45$^{0}$ nên tan73$^{0}$20' < tan45$^{0}$

d, Vì 20$^{0}$ < 37$^{0}$40' nên cot20$^{0}$ > cot37$^{0}$40'