A. PHƯƠNG PHÁP GIẢI

1. Tính diện tích xung quanh - Diện tích toàn phần, thể tích hình trụ hoặc các yếu tố liên quan

Ta làm theo các bước sau:

- Xác định công thức với yêu cầu bài toán

- Tìm R và h

- Thay giá trị và tính

Ví dụ 1: a) Tính diện tích xung quanh của một hình trụ có chu vi đường tròn đáy là 13cm và chiều cao là 3cm.

b) Thể tích của hình trụ có bán kính hình tròn đáy là 5mm và chiều cao là 8mm

Hướng dẫn:

a) Áp dụng công thức S_xq = $2\pi Rh$

Do R = h và S_xq = 314cm$^{2}$ nên ta có $2\pi R^{2}=314$

$\Leftrightarrow R^{2}=\frac{314}{2.3,14}=50$

$\Leftrightarrow R=\sqrt{50}=7,07(cm)$

b) Thể tích của hình trụ là:

V = $\pi R^{3}=\pi 7,07^{3}\approx 1110 (cm^{3})$

2. Tính diện tích xung quanh, thể tích của một hình hỗn hợp gồm nhiều hình

Ta tính diện tích xung quanh hoặc thể tích của từng bộ phận rồi cộng lại hoặc trừ đi.

Ví dụ 2: Một vật có dạng hình trụ, bán kính đáy và chiều cao đều bằng 2R. Người ta khoan một lỗ có bán kính đáy bằng R và chiều cao 2R. Tính thể tích phần vật thể còn lại.

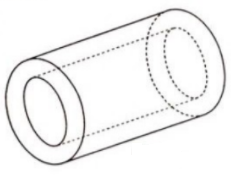
Hướng dẫn:

Thể tích vật thể hình trụ là:
V₁ = $\pi (2R)^{2}.2R = 8\pi R^{3}$

Thể tích lỗ khoan hình trụ là:

V₂ = $\pi R^{2}.2R = 2\pi R^{3}$

Vậy phần thể tích vật còn lại là:

V = V₁ - V₂ = $8\pi R^{3}-2\pi R^{3}=6\pi R^{3}$