A. PHƯƠNG PHÁP GIẢI

1. Tính diện tích xung quanh, thể tích hình nón, nón cụt và các đại lượng có liên quan nếu biết hai trong ba yếu tố: bán kính đáy, chiều cao, đường sinh

- Ta xác định công thức tính.

- Tìm yếu tố còn lại nhờ hệ thức lượng trong tam giác vuông.

- Thay giá trị vào công thức rồi tính.

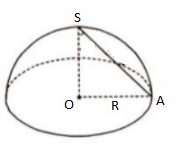
Ví dụ 1: Tính diện tích xung quanh và thể tích của một hình nón khi quay tam giác vuông cân SOA có cạnh huyền SA = 3cm quanh cạnh góc vuông SO cố định.

Hướng dẫn:

Áp dụng công thức S_xq = $\pi Rl$

Vì đường sinh l = SA = 3cm nên ta còn phải tính R = OA

$\Delta $SOA vuông cân tại O nên $SO = OA=\frac{SA}{\sqrt{2}}$ (cm)

$\Rightarrow R = OA = SO = \frac{3\sqrt{2}}{2}$ (cm)

Vậy diện tích xung quanh của hình nón là:

S_xq = $\pi .\frac{3\sqrt{2}}{2}.3=\frac{9\pi \sqrt{2}}{2}(cm^{2})$ 

Thể tích của hình nón là:

V = $\frac{1}{3}\pi \left ( \frac{3\sqrt{2}}{2} \right )^{2}.\frac{3\sqrt{2}}{2}=\frac{9\pi \sqrt{2}}{4}(cm^{3})$

Ví dụ 2: Một hình nón cụt có các bán kính đáy là 6cm và 9cm, chiều cao bằng 4cm.

a) Tính diện tích xung quanh của hình nón cụt.

b) Tính thể tích của hình nón sinh ra hình nón cụt đó.

Hướng dẫn:

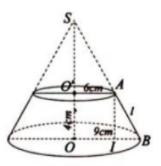
a) Áp dụng công thức Sxq = $\pi (R_{1}+R_{2})l$

Với R1 = 6cm, R2 = 9cm và l = AB

Kẻ AI $\perp $ OB thì tứ giác OO'AI có ba góc vuông nên là hình chữ nhật, dó đó:

AI = OO' = 4cm và IB = 9 - 6 = 3 (cm)

Áp dụng định lý Py-ta-go cho $\Delta $AIB vuông tại I ta được:

$AB^{2}=BI^{2}+IA^{2}=3^{2}+4^{2}=5^{2}$

$\Leftrightarrow AB = 5(cm)$

Vậy S_xq = $\pi (6+9).5=75\pi (cm^{2})$

b, Áp dụng công thức: V = $\frac{1}{3}\pi R^{2}h$ trong đó R = 9cm và chiều cao h = SO

Gọi SO' = x (cm, x > 0) thì h = x + 4

Áp dụng hệ quả định lí Ta-lét cho O'A // OB thu được:

$\frac{SO'}{SO}=\frac{O'A}{OB}$ hay $\frac{x}{x+4}=\frac{6}{9}=\frac{2}{3}$

$\Rightarrow \frac{x}{2}=\frac{x+4}{3}=\frac{x+4-x}{3-2}=4$

$\Leftrightarrow x=8$ nên h = 12 (cm)

Vậy V = $\frac{1}{3}\pi .9^{2}.12=324\pi (cm^{2})$

2. Tính diện tích xung quanh, thể tích của một hình hỗn hợp gồm nhiều hình

Ta tính diện tích xung quanh hoặc thể tích của từng bộ phận rồi cộng lại hoặc trừ đi.

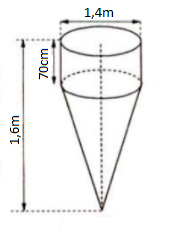
Ví dụ 3: Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 286. Hãy tính:

a) Thể tích của dụng cụ này.

b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).

Hướng dẫn:

Dụng cụ này gồm hai bộ phận:

- Bộ phận hình trụ có bán kính đáy R = 0,7m, chiều cao h = 0,7m.

- Bộ phận hình nón có R = 0,7m, h = 0,9m và đường sinh l = $\sqrt{0,7^{2}+0,9^{2}}=\sqrt{1,3}$ (m)

a) Thể tích của dụng cụ này bằng tổng thể tích của hình trụ và hình nón.

V = $\pi .0,7^{2}.0,7+\frac{1}{3}\pi .0,7^{2}.0,9=0,49\pi (m^{3})$

b) Diện tích mặt ngoài là tổng diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón:

S = $2\pi .0,7.0,7+\pi .0,7.\sqrt{1,3}\approx 5,58(m^{2})$