Bài tập về tính diện tích xung quanh, thể tích hình nón, nón cụt và các đại lượng có liên quan nếu biết hai trong ba yếu tố: bán kính đáy, chiều cao, đường sinh

1. Áp dụng công thức V = $\frac{1}{3}\pi R^{2}h$ có R = 5cm ta còn phải tính h = SO.

Từ giả thiết ta có:

S_xq = $\pi Rl=65\pi \Leftrightarrow l=\frac{65\pi }{5\pi }=13(cm)$

Áp dụng định lý Py-ta-go vào $\Delta $SOA vuông tại O ta được:

$SA^{2}=AO^{2}+OS^{2}$ hay $13^{2}=5^{2}+h^{2}$

$\Leftrightarrow h=12$

Vậy thể tích của hình nón là:

V = $\frac{1}{3}\pi .5^{2}.12=100\pi (cm^{3})$

2.

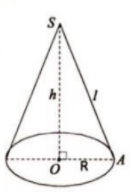
a) Áp dụng định lý Py-ta-go vào $\Delta $SAO vuông tại O ta được:

$l^{2}=R^{2}+h^{2}$ hay $h^{2}=l^{2}-R^{2}=17^{2}-R^{2}$

Lại có S_xq = $\pi Rl=136\pi $ hay R = $\frac{136\pi }{\pi .17}=8$ (cm)

Nên $h^{2}=17^{2}-8^{2}=15^{2}\Leftrightarrow h=15cm$ (vì h>0)

b) Vì S_tp = S_xq + S_đáy nên S_tp = $136\pi +64\pi =200\pi (cm^{2})$

Thể tích của hình chóp là:

V = $\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi .8^{2}.15=320\pi (cm^{3})$

3. 

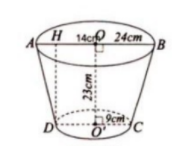
a) Thể tích của xô là:

V = $\frac{1}{3}\pi h(R_{1}^{2}+R_{2}^{2}+R_{1}.R_{2})$

  = $\frac{1}{3}\pi .23.(14^{2}+9^{2}+14.9)\approx 9702 (cm^{3})$

Vậy dung tích của xô là $9702 (cm^{3})$

b) Diện tích tôn để làm xô chính là Sxq của nón cụt cộng với diện tích đáy nhỏ. Mà Sxq = $\pi (R_{1}+R_{2})l=23\pi l$ và diện tích đáy nhỏ là:

S_đáy = $\pi .9^{2}=81\pi (cm^{2})$

Ta cần tìm đường sinh l = AD.

Áp dụng định lý Py-ta-go cho $\Delta $AHD vuông tại H ta được:

$AD^{2}=DH^{2}+HA^{2}$ hay $l^{2}=23^{2}+5^{2}\Leftrightarrow l\approx 23,5(cm)$

Do đó S_xq = $23\pi .23,5= 540,5\pi (cm)$

Vậy diện tích tôn để làm xô là:

S = $540,5\pi +81\pi =621,5\pi (cm^{2})$