Bài tập về tính diện tích xung quanh, thể tích của một hình hỗn hợp gồm nhiều hình
5. Một chi tiết máy có dạng hình hộp chữ nhật có các kích thước là 20cm, 20cm, 5cm. Người ta khoan một lỗ hình trụ có đường kính đáy 16cm và chiều cao 5cm xuyên qua chi tiết đó. Tính thể tích phần vật thể còn lại.
6. Một chi tiết máy có dạng hình trụ có đường kính đáy 25cm, chiều cao 5cm. Người ta khoét một hình hộp chữ nhật có kích thước là 16cm, 16cm, 5cm xuyên qua chi tiết đó. Tính thể tích phần vật thể còn lại.
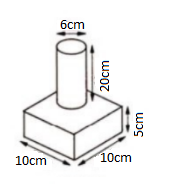
7. Một chi tiết máy có các kích thước như hình vẽ. Hãy tín thể tích và diện tích bề mặt của chi tiết đó.
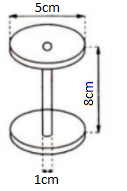
8. Lõi của một cuộn chỉ có kích thước như hình dưới. Tính thể tích của chỉ sau khi được cuộn đầy vào lõi (làm tròn đến số thập phân thứ 2).
5. Thể tích của hình hộp chữ nhật là:
V1 = 20.20.5 = 2000 (cm$^{3}$)
Thể tích của lỗ khoan hình trụ là:
V2 = $\pi .8^{2}.5=320\pi (cm^{3})$
Thể tích phần vật thể còn lại là:
V = V1 - V2 = 2000 - $320\pi \approx 1300,2(cm^{3})$
6. Thể tích vật thể hình trụ là:
V1 = $\pi \left ( \frac{25}{2} \right )^{2}.5=781,25\pi (cm^{3})$
Thể tích của hình hộp chữ nhật là:
V2 = 16.16.5 = 1280 ($cm^{3}$)
Thể tích vật thể còn lại là:
V = V1 - V2 = $781,25\pi - 1280 \approx 1173,13(cm^{3})$
7.

- Chi tiết máy gồm hai hình:
Hình trụ có bán kính đáy R = 3cm, chiều cao h = 20cm nên có thể tích:
V1 = $\pi .3^{2}.20=180\pi (cm^{3})$
Hình hộp chữ nhật có ba kích thước là 10cm, 10cm, 5cm nên có thể tích :
V2 = 10.10.5 = 500 $(cm^{3})$
Vậy thể tích của chi tiết máy này là:
V = V1 + V2 = $180\pi +500\approx 1065,2(cm^{3})$
- Diện tích xung quanh của hình trụ là:
S1 = $2\pi .3.20=120\pi (cm^{2})$
Diện tích xung quanh của hình hộp chữ nhật là:
S2 = 2.(10+10).5 = 200 (cm^{2})$
Tổng diện tích các mặt ngoài còn lại là:
S3 = $\pi .3^{2}+2.10^{2}-\pi .3^{2}=200(cm^{2})$
Vậy tổng diện tích bề mặt của chi tiết là:
S = $120\pi +200 + 200\approx 776,8(cm^{2})$
8.

Thể tích của chỉ sau khi được cuộn đầy là hiệu hai thể tích của hai hình trụ.
Hình trụ thứ nhất có bán kính đáy là R1 = 2,5cm, chiều cao là 8cm nên có thể tích:
V1 = $\pi .2,5^{2}.8=50\pi (cm^{3})$
Hình trụ thứ hai là lõi có bán kính đáy là R2 = 0,5cm và chiều cao là 8cm nên có thể tích :
V2 = $\pi .0,5^{2}.8=2\pi (cm^{3})$
Vậy thể tích của chỉ sau khi được cuộn đầy là:
V = V1 - V2 = $50\pi -2\pi =48\pi \approx 150,72(cm^{3})$
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận