Slide bài giảng Toán 8 kết nối: Luyện tập chung (tr.62)

Tóm lược nội dung

LUYỆN TẬP CHUNG

Bài 3.19 (Trang 63):

Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?

Trả lời rút gọn:

a) Tứ giác ABCD là hình bình hành vì có các góc đối bằng nhau.

b) Tứ giác ABCD không phải là hình bình hành vì các góc đối ở đỉnh B và D không bằng nhau.

c) Tứ giác ABCD có các cạnh đối AD và BC song song (cùng tạo với đường thẳng DC hai góc ở vị trí đồng vị bằng nhau), AD = BC nên là hình bình hành.

Bài 3.20 (Trang 63):

Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:

a) AN = CM;

b) = .

Trả lời rút gọn:

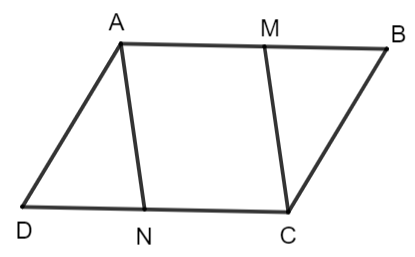
a) Tứ giác AMCN có hai cạnh đối AM, CN song song và bằng nhau nên AMCN là hình bình hành

AN = CM

b) Vì AMCN là hình bình hành, hai và là hai góc đối của hình bình hành 

Bài 3.21 (Trang 63):

Vẽ tứ giác ABCD theo hướng dẫn sau:

Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.

Bước 2. Lấy điểm C a.

Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.

Hãy giải thích tại sao tứ giác ABCD là hình bình hành.

Trả lời rút gọn:

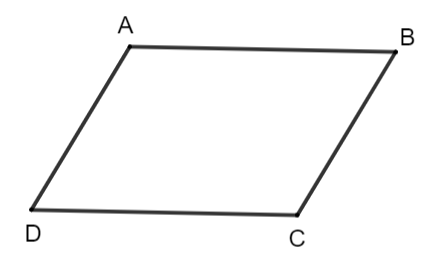
Do đường thẳng CD//AB và A, D nằm cùng phía đối với đường thẳng BC nên ABCD là một tứ giác (lồi). Vì hai cạnh đối AB và CD của tứ giác đó song song và bằng nhau nên nó là một hình bình hành.

Bài 3.22 (Trang 63):

Cho hình bình hành ABC có AB = 3 cm, AD = 5 cm. 

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C

Trả lời rút gọn:

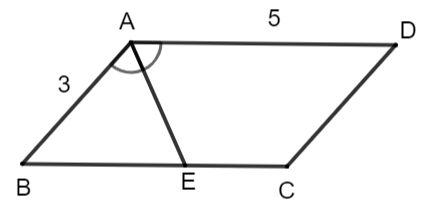
Do BC = AD = 5cm nên có điểm E duy nhất trên cạnh BC sao cho BE = 3cm

Ta có BE = BA nên BAE cân tại B

Mà (so le trong)

Suy ra

Vậy AE là tia phân giác của góc A của hình bình hành ABCD.

Tia này không cắt cạnh CD.

b) Ta có EC = BC – BE = 5 – 3 = 2 cm.

Bài 3.23 (Trang 63):

Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:

a) Hai tứ giác AEFD, ABFC là những hình bình hành;

b) Các trung điểm của ba doạn thẳng AF, DE, BC trùng nhau.

Trả lời rút gọn:

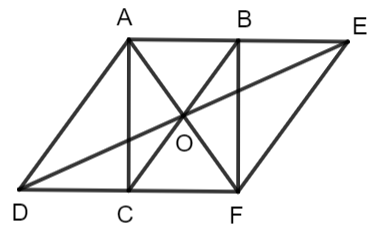
a) B là trung điểm của AE nên AE = AB + BE = AB 2

C là trung điểm của DF nên DF = DC + CF = DC 2

Do ABCD là hình bình hành nên AB = DC, AB // DC

Suy ra AE = DF, AE // DF AEFD là hình bình hành

Vì AB = ; CF = ; AB = DC nên AB = CF

AE // DF AB // CF

ABFC là hình bình hành

b) AEFD là hình bình hành có AF và DE đường chéo nên AF và DE cắt nhau tại O; O là trung điểm của AF và DE.

ABFC là hình bình hành có AF và BC đường chéo nên AF và BC cắt nhau tại O; O là trung điểm của AF và BC

Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Bài 3.24 (Trang 63):

Cho ba điểm không thẳng hàng.

a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy vẽ hình và mô tả cách tìm

b) Hỏi tìm được bao nhiêu điểm như vậy?

Trả lời rút gọn:

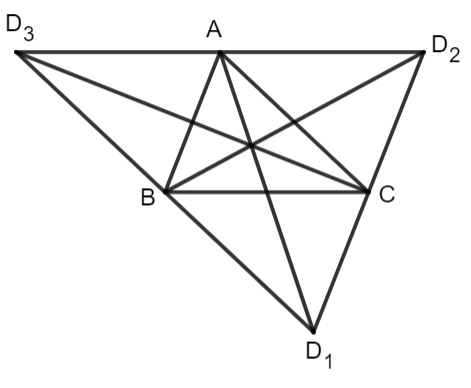
a) Bốn điểm ABCD là hình bình hành, có AD và BC là đường chéo thì AD và BC cắt nhau tại trung điểm mỗi đường. Từ trung điểm BC kẻ đoạn thẳng đối xứng với điểm A qua trung điểm ta được điểm D.

b) Vì có 3 điểm A, B, C nên tìm được 3 điểm D như vậy.