Slide bài giảng toán 8 kết nối bài: Luyện tập chung chương III (1 tiết)

Tóm lược nội dung

LUYỆN TẬP CHUNG

Bài 3.9 (Trang 56):

Tứ giác ABCD trong hình 3.25 có phải là hình thang không? Vì sao?

Trả lời rút gọn:

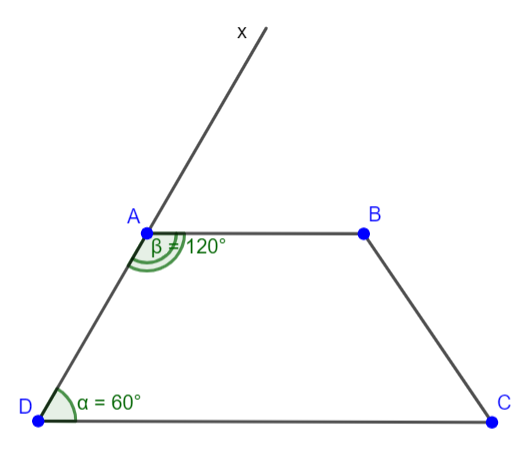
Ta có tứ giác ABCD có và bù nhau. Gọi Ax là tia đối của tia AD thì:

=> AB // DC (hai dóc đồng vị bằng nhau)

Vậy ABCD là hình thang với hai đáy AB và CD.

Bài 3.10 (Trang 56):

Cho hình thang cân ABCD (AB//CD) có AB = AD. Biết góc = 30, tính số đo các các góc của hình thang đó. 

Trả lời rút gọn:

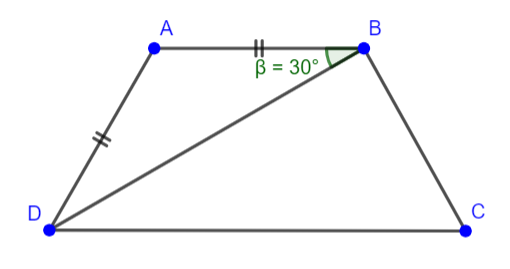
Ta có cân tại A (AB = AD (gt)) => .

Vì AB // CD nên (so le trong).

=> .

Mà ABCD là hình thang cân nên ; .

Bài 3.11 (Trang 56):

Tính số đo các góc của tứ giác ABCD trong hình 3.26.

Trả lời rút gọn:

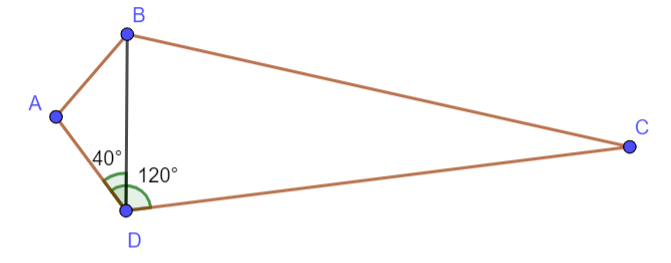
cân tại A nên .

Trên hình, ; nên

cân tại C nên

Tứ giác ABCD có .

Bài 3.12 (Trang 56):

Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BD, CA, tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân.

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB +MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Trả lời rút gọn:

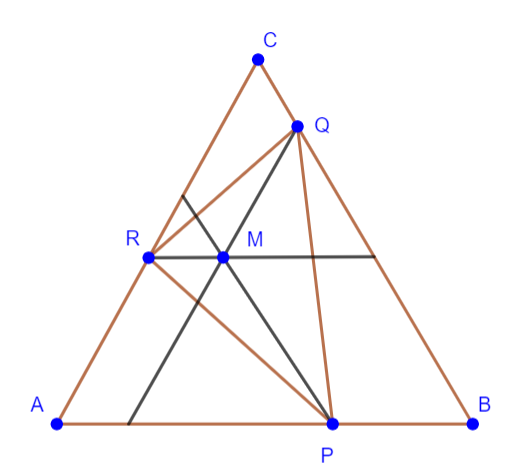
a) Tứ giác APMR là hình thang do MR // AP.

Có (do MP // CB) nên APMR là hình thang cân.

b) Tương tự câu a, ta có các tứ giác BQMP và CRMQ là những hình thang cân; suy ra RP = MA, PQ = MB, QR = MC (hai đường chéo của hình thang cân). Chu vi của tam giác PQR là: .

c) Tam giác PQR làm tam giác đều có nghĩa là PQ = QR = RP tức là MB = BC = MA. 

Vậy M cách đều ba đỉnh A, B, C tức M là trọng tâm của tam giác đều ABC.