Slide bài giảng toán 8 kết nối bài 11: Hình thang cân (2 tiết)

Tóm lược nội dung

BÀI 11. HÌNH THANG CÂN

I. HÌNH THANG. HÌNH THANG CÂN

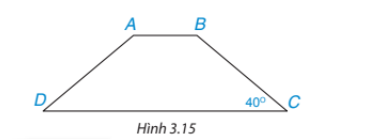
Luyện tập 1 (Trang 53):

Tính các góc của hình thang cân ABCD (AB//CD), biết = 40 (H.3.15).

Trả lời rút gọn:

Vì ABCD là hình thang cân (AB // CD) nên:

Ta có:

=>

=>

II. TÍNH CHẤT CỦA HÌNH THANG

Hoạt động 1 (Trang 53):

Cho hình thang cân ABCD, AB//CD và AB < CD (H.3.16).

a) Từ A và B kẻ AH Chứng minh rằng AH = BI bằng cách chứng mih

b) Chứng minh

Trả lời rút gọn:

a) Ta có AB // CD (gt) mà (gt)

=> . Suy ra .

Xét và có:

(so le trong)

AI chung

=> (g.c.g)

=> AH = BI.

b) Xét và có:

(ABCD là hình thang cân)

AH = BI (theo a)

=> (g.c.g)

=> AD = BC.

Luyện tập 2 (Trang 53):

Cho tứ giác ABCD như hình 3198. Biết rằng .

Chứng minh rằng AD = BC.

Trả lời rút gọn:

Ta có: (gt) mà hai góc này ở vị trí đồng vị, nên suy ra: DC // AB.

Vậy tứ giác ABCD là hình thang.

Lại có => hình thang ABCD cân.

=> AD = BC.

Hoạt động 2 (Trang 54):

Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H3.19). Hãy chứng minh Từ đó suy ra AC = BD.

Trả lời rút gọn:

Xét và có:

CD chung

AD = BC

=> (c.g.c)

=> DC = BD.

Luyện tập 3 (Trang 54):

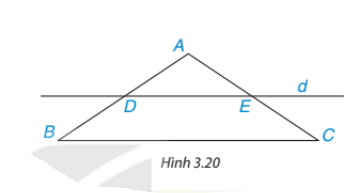
Cho tam giác ABC cân tại A. Kẻ một đường thẳng ở song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).

a) Tứ giác DECB là hình gì?

b) Chứng minh BE = CD.

Trả lời rút gọn:

a) Vì DE // BC nên tứ giác DECB là hình thang.

Lại có cân tại A =>

Suy ra hình thang DECB có hai góc kề 1 đáy bằng nhau nên là hình thang cân.

b) Xét và có:

BD = CE (vì DECB là hình thang cân)

BC chung

=> (c.g.c)

=> BE = CD

III. DẤU HIỆU NHẬN BIẾT

Vận dụng (Trang 55):

Hãy giải bài toán mở đầu.

Trả lời rút gọn:

Theo hình 3.11 ta có hình thang mới là:

MN’M’N.

Ta có:

+ Hình thang AMND có: M’N’ là cạnh mới cắt ; AD là cạnh bên.

+ Hình thang MBCN có: MN là cạnh mới cắt; BC là cạnh bên.

=> (so le trong)

=> Lật hình thang AM’N’D để ghép vào hình thang MBCN thì cạnh DA trùng với BC. Thì hình mới là MN’M’N có 

Vậy nó là hình thang cân.

IV. GIẢI BÀI TẬP CUỐI SGK

Bài 3.4 (Trang 55):

Hình thang trong hình 3.23 có là hình thang cân không? Vì sao?

Trả lời rút gọn:

Ta có :

=> ; Mà

Nên suy ra hình thang ABCD không phải hình thang cân.

Bài 3.5 (Trang 55):

Cho hình thang ABCD (AB//CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Trả lời rút gọn:

Gọi

Xét hai tam giá vuông và có :

Suy ra (cạnh huyền – cạnh góc vuông)

=> CH = DH (1).

Ta có : (do )

=> EH là phân giác của .

=> (do AB // CD).

Gọi

Xét tam giác vuông BHK và AHK có :

=> (cạnh góc vuông-góc nhọn)

=> BH = AH (2)

Từ (1)(2) => AC = BD

=> Hình thang ABCD là hình thang cân.

Bài 3.6 (Trang 55):

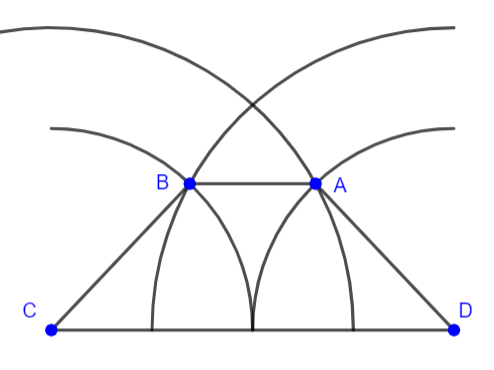
Vẽ hình thang cân ABCD (AB//CD) biết đáy lớn CD dài 4cm, cạnh bên dài 2cm và đường chéo dài 3cm.

Trả lời rút gọn:

- Vẽ đáy lớn CD = 4 cm

- Vẽ cung tròn tâm C bán kính 2 cm, cung tròn tâm D bán kính 3 cm, giao điểm của 2 cung tròn là B

- Tương tự, vẽ cung tròn tâm D bán kính 2cm, cung tròn tâm C bán kính 3 cm, giao điểm của 2 cung tròn là A

(Tất cả cung tròn đều nằm trên cùng 1 nửa mặt phẳng bờ CD).

Bài 3.7 (Trang 55):

Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB//CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Trả lời rút gọn:

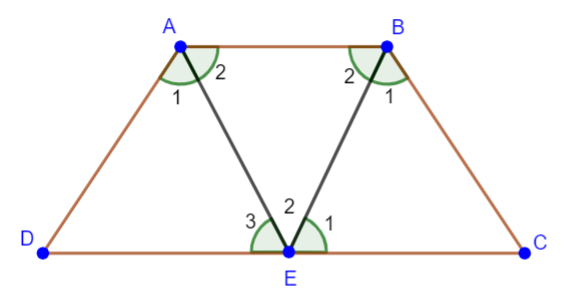
+ Ta có: Hình thang ABCD cân và AE, BE là phân giác và

+ Lại có: (so le trong)

=> cân tại C, nên BC = EC (1).

=> cân tại C, nên AD = ED (2).

Vì ABCD là hình thang cân nên AD = BC, từ (1)(2) suy ra: EC = ED.

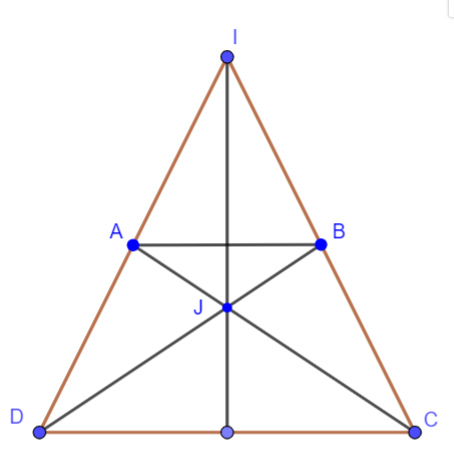
Bài 3.8 (Trang 55):

Hình thang cân ABCD (AB//CD, AB//CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Trả lời rút gọn:

Xét và có:

AD = BC (tính chất hình thang cân)

CD chung

AC = BD (đường chéo hình thang cân)

=> (c.c.c)

=> hay => cân tại I

Do đó JD = JC (1)

có hai góc ở đáy bằng nhau nên cân tại I.

=> ID = IC (2)

Từ (1)(2) suy ra IJ là trung trực của CD.

Chứng minh tương tự ta có: JA = JB; IA = IB

Suy ra J và I cùng thuộc đường trung trực của đoạn thẳng AB

Do đó, IJ là đường trung trực của AB.