Slide bài giảng Toán 8 kết nối: Bài tập cuối chương III

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG III

I. TRẮC NGHIỆM

Câu 3.39 (Trang 74):

Trong các khẳng định sau, khẳng định nào đúng?

A. Không có tứ giác nào mà không có góc tù.

B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.

C. Nếu tứ giác có hai góc tù thì haigóc còn lại phải nhọn.

D. Không có tứ giác nào có ba góc tù.

Trả lời rút gọn:

Tứ giác có ba góc nhọn thì tổng số đo của ba góc bé hơn .

Khi đó, góc còn lại sẽ lớn hơn .

Do đó, góc còn lại là góc tù nên khẳng định B đúng.

Câu 3.40 (Trang 74):

Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.

b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.

c) Tứ giác có ba góc vuông là hình chữ nhật.

d) Tứ giác có ba cạnh bằng nhau là hình thoi.

Trả lời rút gọn:

A. Sai. Vì tứ giác có hai đường chéo bằng nhau là hình thang cân.

B. Đúng. Vì theo dấu hiệu nhận biết tứ giác có hai cặp cạnh bằng nhau là hình bình hành.

C. Đúng. Vì theo dấu hiệu nhận biết tứ giác có ba góc vuông là hình chữ nhật.

D. Sai. Vì tứ giác có bốn cặp cạnh bằng nhau là hình thoi.

Câu 3.41 (Trang 74):

Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.

Trả lời rút gọn:

A. Đúng. Vì tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

B. Đúng. Vì theo dấu hiệu nhận biết tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.

C. Đúng. Vì tứ giác có hai cạnh đối song song là hình thang.  Hình thang có hai đường chéo bằng nhau nên tứ giác đó là hình thang cân.

D. Sai. Vì tứ giác có hai cạnh song song và bằng nhau là hình bình hành

II. TỰ LUẬN

Bài 3.42 (Trang 74):

Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.

Trả lời rút gọn:

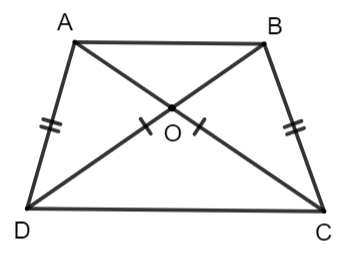
Ta có tứ giác ABCD có hai đường chéo AC = BD, hai cạnh đối AD = BC.

Xét ADC và BCD có : AD = BC, DC chung, AC = BD

Suy ra ADC = BCD (c.c.c)

ODC cân tại O (1)

Chứng minh tương tự, ta có : ABC = BAD (c.c.c)

OAB cân tại O (2) 

Mặt khác (đối đỉnh) (3)

Từ (1), (2), (3) suy ra

AB // DC (so le trong)

ABCD là hình thang

Lại có AC = OA + OC = OB + OD = BD nên ABCD là hình thang cân.

Bài 3.43 (Trang 74):

Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2AB.

a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?

b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.

Trả lời rút gọn:

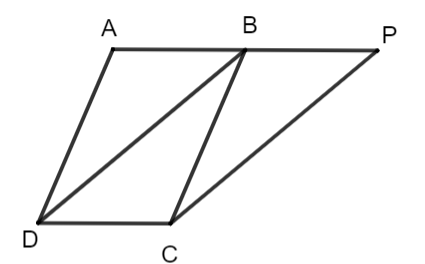
a) Ta có P trên tia AB, AP = 2AB suy ra AB = BP

ABCD là hình bình hành nên AB // CD, P nằm trên tia AB 

Suy ra BP // CD,

Tứ giác BPCD có BP // CD, BP = CD (= AB)

BPCD là hình bình hành.

b)  Tam giác ABD vuông cân tại A thì ABCD là hình vuông

Hình bình hành BPCD có suy ra ,