Slide bài giảng toán 8 kết nối bài 10: Tứ giác (1 tiết)

Tóm lược nội dung

BÀI 10. TỨ GIÁC

I. TỨ GIÁC LỒI

Luyện tập 1 (Trang 49):

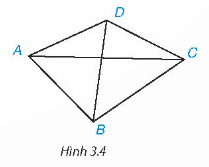
Quan sát tứ giác ABCD trong Hình 3.4.

Hai đỉnh không cùng một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.

Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.

Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

Trả lời rút gọn:

Đường chéo còn lại là BD.

Cặp cạnh AD, BC cũng là cặp cạnh đối.

Cặp góc B, D cũng là cặp góc đối.

II. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC

Hoạt động (Trang 50):

Cho tứ giác ABCD. Kẻ đường chéo BD (H3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với các tam giác ABD và CBD, tính tổng của tứ giác ABCD.

Trả lời rút gọn:

- Áp dụng định lí tổng ba góc trong một tam giác ta có;

+ có:

+ có;

Mà ta có: 

Luyện tập 2 (Trang 50):

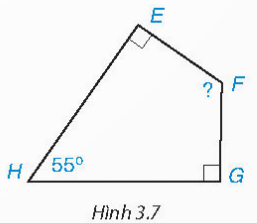
Cho tứ giác EFGH như hình 3.7, hãy tính góc F 

Trả lời rút gọn:

Xét tứ giác EFGH có:

+

+

Mà theo định lí ta có:

Suy ra:

Vậy  

Vận dụng (Trang 50):

Giải bài oán ở mở đầu

Trả lời rút gọn:

- Có thể ghép được 4 tứ giác khít nhau như hình.

- Khi xếp khít nhau, có 1 điểm chung tại 4 đỉnh của 4 tứ giác. Tổng số đo góc của 4 góc đó bằng 360º.

III. GIẢI BÀI TẬP CUỐI SGK

Bài 3.1 (Trang 51):

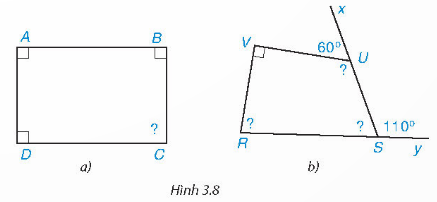
Tính góc chưa biết của các tứ giác trong hình 3.8

Trả lời rút gọn:

a) .

b)

Bài 3.2 (Trang 51):

Tính góc chưa biết của tứ giác trong hình 3.9 biết rằng .

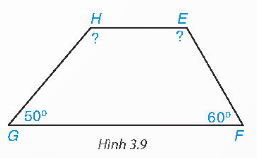
Trả lời rút gọn:

Ta có :

(1)

Mà , thay vào (1) ta có :

Bài 3.3 (Trang 51):

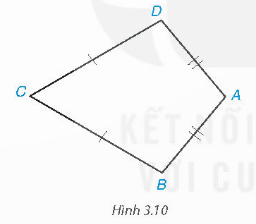
Tứ giác ABCD trong hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.

b) Tính các góc B, D biết rằng = 100, = 60.

Trả lời rút gọn:

a) Nối AC và BD cắt nhau tại E.

+ Xét có AD = AB (gt), suy ra cân tại A

Suy ra đường trung trục của BD đi qua điểm A (1).

+ Xét có CB = CD (gt), suy ra cân tại C

Suy ra đường trung trực của BD đi qua điểm C (2).

Từ (1)(2) suy ra AC là trung trực của BD.

b) Xét và có:  => = (c.c.c)

Suy ra

Ta có:

Suy ra

Vậy

Suy ra .