Slide bài giảng toán 10 kết nối bài: Bài tập cuối chương III

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG III 

A.TRẮC NGHIỆM

Bài 3.12: Cho tam giác ABC có .Khẳng định nào sau đây là đúng?

Trả lời rút gọn: 

Bài 3.13: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

Trả lời rút gọn: 

a. B                       b. A

2. TỰ LUẬN

Bài 3.14: Tính giá trị của các biểu thức sau: 

a. M = sin45^o .cos45^o + sin30^o

b. N = sin60^o.cos30^o + 12sin 45^o.cos 45^o

c. P = 1 + tan²60^o

d. Q =  1sin² 120^o−cot² 120^o.

Trả lời rút gọn: 

a)

b. N = sin60^o.sin60^o + sin 45^o.sin45^o

        = +

c. 

P = 1 + ()² = 4

d) .

Bài 3.15 : Cho tam giác ABC có  AC = 10. Tính a, R, S, r.

Trả lời rút gọn: 

Do nên

Theo định lí sin

=> .

Từ đó, vì nên

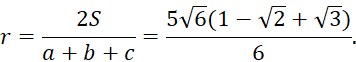
Bài 3.16 :  Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a. =0

b.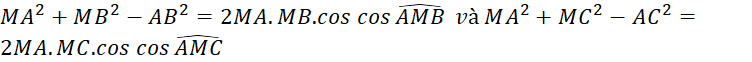 

c.. (công thức đường trung tuyến).

Trả lời rút gọn: 

a) 

Hai góc và bù nhau nên hay.

b) Áp dụng định lí côsin cho tam giác :

Áp dụng định lí côsin cho tam giác AMC có:

c) Từ kết quả câu b suy ra:

=>

=> .

Bài 3.17 : Cho tam giác ABC. Chứng minh rằng:

a. Nếu góc A nhọn thì b² + c² > a²

b. Nếu góc A tù thì b² + c² < a²

c. Nếu góc A vuông thì b² + c² = a²

Trả lời rút gọn: 

Áp dụng định lí cosin cho tam giác ABC có:

 a² = b² + c²  - 2bc.cos A

a. Nếu góc A nhọn => 2.b.c.cos A >0 

=>  a² = b² + c²  - 2bc.cos A < b² + c²

b. Nếu góc A tù => 2.b.c.cos A <0 

=>  a² = b² + c²  - 2bc.cos A > b² + c²

c. Nếu góc A vuông => 2.b.c.cos A =0 

=>  a² = b² + c²  - 2bc.cos A = b² + c²

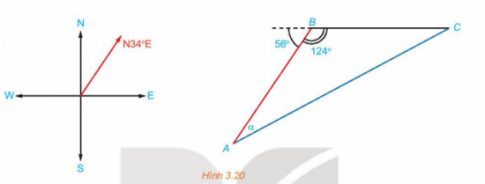
Bài 3.18 :  Trên biển, tàu B ở vị trí cách tàu A 53km về hướng N34^oE. Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.

a. Hỏi tàu A cần phải chuyển động theo hướng nào?

b. Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?

Trả lời rút gọn: 

a) Giả sử sau giờ, tàu gặp tàu ở điểm . 

Khi đó .

 Do tàu ở vị trí cách tàu về hướng và tàu chạy về hướng đông nên . 

Đặt . Khi đó, tàu chạy từ , theo hướng .

Áp dụng định lí sin cho tam giác => => . Do đó, tàu cần chạy theo hướng để gặp tàu .

b) 

Áp dụng định lí sin cho tam giác ,

Vậy sau 2 giờ chạy theo hướng thì tàu gặp tàu .

Bài 3.19 : Trên sân bóng chày cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4. Vị trí đứng ném bóng (Pitcher's mound) nầm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Trả lời rút gọn: 

Gọi theo thứ tự là vị trí gôn Nhà, gôn 1, gôn 2, gôn 3 

 gọi P là vị trí đứng ném bóng (như hình vẽ).

Ta có và .

 Áp dụng định lí côsin cho tam giác FHP

=> .

Do đó khoảng cách từ vị trí đứng ném bóng đến gôn 1 và gôn 3 xấp xỉ bằng .

T.