Slide bài giảng toán 10 kết nối bài 10: Vectơ trong mặt phẳng tọa độ

Tóm lược nội dung

BÀI 10. VECTƠ TRONG MẶT PHẲNG TỌA ĐỘ

1. TỌA ĐỘ CỦA VECTƠ

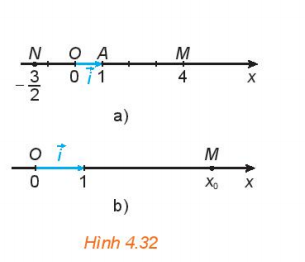
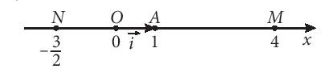
Bài 1: Trên trục số Ox, gọi A là điểm biểu diến số 1 và đặt .  (H4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số Hãy biểu thị mỗi vectơ   và theo vecto .

Trả lời rút gọn: 

Do A biểu diễn số 1, M biểu diễn số 4, nên hai vectơ và có cùng phương, cùng hướng và .

=> .

Do A biểu diễn số 1, N biểu diễn số nên hai vectơ và có cùng phương, ngược hướng và .

=> .

Bài 2: Trong Hình 4.33:

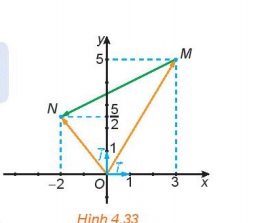
a. Hãy biểu thị mỗi vectơ  theo các vectơ

b. Hãy biểu thị vectơ theo các vectơ từ đó biểu thị vectơ theo các vectơ

Trả lời rút gọn: 

a)

 .

b) 

.

Bài 3: Tìm tọa độ của

Trả lời rút gọn: 

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

Bài 1: Trong mặt phẳng tọa độ Oxy, cho  = (2; -3), = (4;1), = (8;-12).

a. Hãy biểu thị mỗi vectơ  , , . theo các vectơ

b. Tìm tọa độ của các vectơ  + ,

c. Tìm mối liên hệ giữa hai vectơ , 

Trả lời rút gọn: 

a) .

b) Vì

=> .

.

=> .

c) Vì và 

nên .

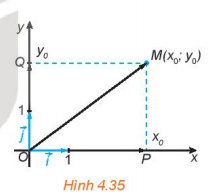
Bài 2: Trong mặt phẳng tọa độ Oxy, cho điểm M(x_o; y_o). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy.

a. Trên trục Ox, điểm P biểu diễn số nào? Biểu thị theo và tính độ dài của theo x_o.

b. Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị theo và tính độ dài của theo y_o.

c. Dựa vào hình chữ nhật OPMQ, tính độ dài của theo x_o; y_o.

d. Biểu thị theo các vectơ .

Trả lời rút gọn: 

a) 

.

b) 

.

c) Hình chữ nhật OPMQ có độ dài hai cạnh OP = |x_o| và OQ = |y_o|

.

d) .

Bài 3: Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x'; y').

a. Tìm tọa độ của các vectơ 

b.Biểu thị vectơ theo các vectơ và tìm tọa độ của

c. Tìm độ dài của vectơ

Trả lời rút gọn: 

a) 

, .

b) 

=> .

c) 

.

Bài 4 : Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1). B(3; 3).

a. Các điểm O, A, B có thẳng hàng hay không?

b. Tìm điểm M(x; y) để OABM là một hình bình hành.

Trả lời rút gọn: 

a) Hai vectơ và không cùng phương (vì ). 

A, B, O không cùng nằm trên một đường thẳng=> chúng không thẳng hàng.

b) 

OABM là một hình bình hành ⇔

và

.

=> M(1; 2).

Bài 5 : Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.

Trả lời rút gọn: 

.

  hay .

=> x = 14,025 và y = 106,8.

M ( 14,025; 106,8)

BÀI TẬP CUỐI SGK

Bài 4.16: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2).

a. Tính độ dài của các đoạn thẳng OM, ON, MN.

b. Chứng minh rằng tam giác OMN vuông cân.

Trả lời rút gọn: 

a) .

b) Do và OM = MN nên tam giác OMN vuông cân tại M.

Bài 4.17: Trong mặt phẳng tọa độ Oxy, cho các vectơ =3 =(4;−1) và các điểm M(-3; 6), N(3; -3).

a. Tìm mối liên hệ giữa các vectơ

b. Các điểm O, M, N có thẳng hàng hay không?

c. Tìm điểm P(x; y) để OMNP là một hình bình hành.

Trả lời rút gọn: 

a)

=> .

.

Vì nên .

b) và . 

Do nên hai vectơ và không cùng phương. 

Do đó O, M, N không thẳng hàng.

c) Giả sử tìm được điểm P sao cho OMNP là một hình bình hành.

 Khi đó  

=> P(6; -9) là điểm cần tìm.

Bài 4.18: Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2).

a. Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.

b. Tìm tọa độ trung điểm M của đoạn thẳng AB.

c. Tìm tọa độ trọng tâm G của tam giác ABC.

d. Tìm điểm D(x; y) để O(0; 0) là trọng tâm của tam giác ABD.

Trả lời rút gọn: 

Từ giả thiết suy ra và

a) Vì nên các vectơ và không cùng phương

=> A, B, C là ba đỉnh của một tam giác.

b)

=>  .

c)

=>  .

d)

=> D(-3; -7).

Bài 4.19: Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau:

Tàu khởi hành từ vị trí A(1;2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ =(3;4). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.

Trả lời rút gọn: 

=. 

Gọi B(x; y) là điểm biểu diễn vị trí của tàu tại thời điểm sau khi khởi hành 1,5 giờ.

Khi đó do nên 

Vậy sau 1,5 giờ tàu đến vị trí điểm B(5,5; 8).

Bài 4.20 : Trong Hình 4.38, quân mã đang ở vị trí có tọa độ (1;2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?

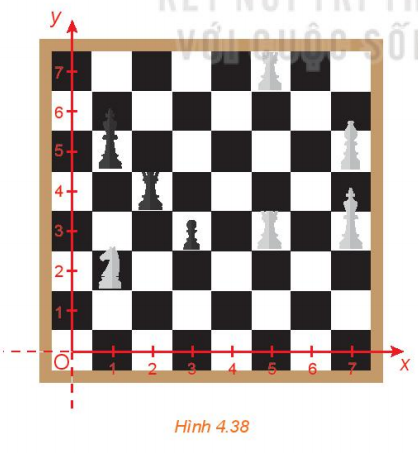
Trả lời rút gọn: 

- Quân mã đi theo hình chữ L:

• hoặc tiến 1 ô rồi sang trái (hoặc phải) 2 ô

• hoặc tiến 2 ô rồi sang trái (hoặc phải 1 ô).

- Quân mã không bị cản bởi bất cứ quân nào trên đường đi; chỉ bị cản khi ô đích đến là quân cờ cùng màu.

Vậy quân mã ở ô (1; 2) trên bàn cờ được phép di chuyển tới những ô (0; 0), (2;0), (3; 1), (3; 3), (2; 4) và (0; 4).