Slide bài giảng toán 10 kết nối bài 21: Đường tròn trong mặt phẳng toạ độ

Tóm lược nội dung

BÀI 21.ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ

1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R. Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào?

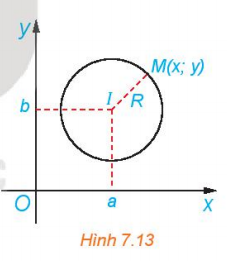
Trả lời rút gọn:

Điểm thuộc đường tròn ⇔ .

Hay:  

Bài 2: Tìm tâm và bán kính của đường tròn (C): (x + 2)² +(y - 4)² = 7.

Trả lời rút gọn:

,

Bài 3: Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.

a. x² + y² - 2x + 4y - 1 = 0

b. x² + y² - 2x + 4y + 6 = 0

c. x² + y² + 6x - 4y  + 2 = 0

Trả lời rút gọn:

a)

Phương trình đã cho là phương trình đường tròn có I(1;-2) và có

b) Phương trình đã cho không là phương trình đường tròn vì

c)

Phương trình đã cho là phương trình đường tròn có I(-3;2) và có

Bài 4: Viết phương trình đường tròn (C) đi qua ba điểm M(4; -5), N(2; -1), P(3; -8).

Trả lời rút gọn:

Gọi điểm là tâm của đường tròn (C) =>

Vì nên ta có hệ phương trình :

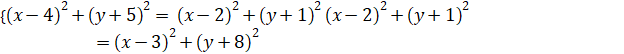
phương trình đường tròn (C):   

Bài 5 : Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn để người bơi có thể ngồi tựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy π=3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai.

Trả lời rút gọn:

Gọi bán kính bể hình tròn và bể nửa hình tròn tương ứng là . 

tổng chu vi ba bể là khi và chỉ khi

Gọi tổng diện tích của ba bể sục là S =>

Trong mặt phẳng toạ độ Oxy: có tâm O(0;0), và đường thẳng . 

Khi đó bài toán được chuyển thành: Tìm R nhỏ nhất để (C) và có ít nhất một điểm chung, với hoành độ và tung độ đều là các số dương.

Mà

Dấu “=” xảy ra khi đường thẳng tiếp xúc với đường tròn (C).

Vậy bán kính của bể nhỏ nhất cần tìm là

2. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

Bài 1: Cho đường tròn (C): (x - 1)² + (y - 2)² = 25 và điểm M(4; -2).

a. Chứng minh điểm M(4; -2) thuộc đường tròn (C).

b. Xác định tâm và bán kính của (C).

c. Gọi Δ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng Δ. Từ đó, viết phương trình đường thẳng Δ.

Trả lời rút gọn:

a) Thay tọa độ điểm M 

(đúng)

Vậy M thuộc đường tròn (C).

b)

có  ,

c) Do là một vectơ pháp tuyến của

Bài 2: Cho đường tròn (C) có phương trình x² + y² - 2x + 4y + 1 = 0. Viết phương trình tiếp tuyến Δ của (C) tại điểm N(1; 0).

Trả lời rút gọn:

Do => điểm N thuộc (C).

Đường tròn (C) có  . 

Tiếp tuyến của (C) tại N có vectơ pháp tuyến là  

Phương trình tiếp tuyến là: hay

Bài 3: Trên mặt phẳng tọa độ Oxy, một vật chuyển động nhanh trên đường tròn có phương trình x² + y² =25.Khi tới vị trí M(3;4) thì vật bị văng khỏi quỹ đạo tròn và ngay sau đó, trong một khoảng thời gian ngắn bay theo hướng tiếp tuyến của đường tròn. Hỏi trong khoảng thời gian ngắn ngay sau khi văng, vật chuyển động trên đường thẳng nào ?

Trả lời rút gọn:

Khi tới vị trí M(3;4), vật bị văng khỏi quỹ đạo tròn và ngay sau đó bay theo hướng tiếp tuyến d của đường tròn tại điểm M.

 Do đó d đi qua điểm M và nhận vectơ làm vectơ pháp tuyến.

d:

BÀI TẬP CUỐI SGK

Bài 7.13: Tìm tâm và tính bán kính của đường tròn: (x + 3)² + (y - 3)² = 36

Trả lời rút gọn:

Bài 7.14: Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.

a. x² + y² + xy + 4x - 2 = 0

b. x² + y² – 2x – 4y + 5 = 0

c. x² + y² + 6x - 8y + 1 = 0

Trả lời rút gọn:

a) không phải là phương trình đường tròn 

b)

Xét:

⇒ Phương trình trên không là phương trình đường tròn.

c) 

Xét: .

⇒ Phương trình trên là phương trình đường tròn, có và

Bài 7.15: Viết phương trình của đường tròn (C) trong mỗi trường hợp sau:

a. Có tâm I(-2; 5) và bán kính R = 7.

b. Có tâm I(1; -2) và đi qua điểm A(-2; 2)

c. Có đường kính AB, với A(-1; -3), B(-3; 5)

d. Có tâm I(1; 3) và tiếp xúc với đường thẳng x + 2y + 3 = 0.

Trả lời rút gọn:

a) Phương trình đường tròn có  và  là:

b)

Phương trình đường tròn là:

c) Vì AB là đường kính của (C) nên (C) có tâm I là trung điểm của AB và

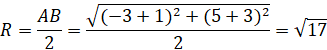
Vậy phương trình của đường tròn (C) là:

d) Gọi (C) là đường tròn có I(1;3) và tiếp xúc với đường thẳng .

.

Vậy phương trình của đường tròn (C) là:

Bài 7.16: Trong mặt phẳng tọa độ, cho tam giác ABC với A(6; -2), B(4; 2), C(5; -5). Viết phương trình đường tròn ngoại tiếp tam giác đó.

Trả lời rút gọn:

Gọi đường tròn ngoại tiếp tam giác ABC có tâm  

Do I là tâm đường tròn ngoại tiếp tam giác ABC nên I cách đều 3 đỉnh A, B, C. Hay

ta có hệ phương trình:

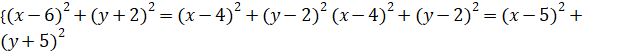
⇒ Đường tròn có 

Vậy phương trình của đường tròn (C) là:

Bài 7.17: Cho đường tròn (C): x² + y² + 2x - 4y + 4 = 0. Viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2).

Trả lời rút gọn:

Do => M thuộc đường tròn (C).

Đường tròn (C) có  .

Tiếp tuyến của (C) tại M có vectơ pháp tuyến là nên phương trình là:

hay .

Bài 7.18: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0≤t≤180) vật thể ở vị trí có tọa độ (2 + sin t^o; 4 + cost^o).

a. Tìm vị trí ban đầu và vị trí kết thúc của vật thể.

b. Tìm quỹ đạo chuyển động của vật thể.

Trả lời rút gọn:

a) Vị trí ban đầu của vật thể là tại thời điểm

 => tọa độ của điểm là:

Vị trí kết thúc của vật thể là tại thời điểm

=>  tọa độ của điểm là:

b) Gọi điểm thuộc vào quỹ đạo chuyển động của vật thể.

và

và

=>  

Vật thể chuyển động trên đường tròn có , R=1 và d=AB

Khi t thay đổi trên đoạn thì thay đổi trên đoạn và thay đổi trên đoạn

=> và .

Vậy quỹ đạo của vật thể (hay tập hợp điểm M) là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm , bờ AB.