Slide bài giảng toán 10 kết nối bài 9: Tích của một số vectơ với một số

Tóm lược nội dung

BÀI 9.TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ

1. TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ

Bài 1: Cho vectơ .Hãy xác định điểm C sao cho

a. Tìm mối quan hệ giữa

b. Vectơ có mối quan hệ như thế nào về hướng và độ dài đối với vectơ ?

Trả lời rút gọn: 

a) Theo quy tắc ba điểm,

Vectơ cùng hướng với vectơ , có độ dài gấp hai lần độ dài của vectơ .

b) Vì và nên B là trung điểm của AC. 

Vectơ cùng hướng với vectơ và độ dài của gấp đôi độ dài của .

Bài 2: có bằng nhau hay không?

Trả lời rút gọn: 

Bài 3: Trên một trục số gọi O, A, M, N tương ứng biểu thị các số 0; 1; Hãy nêu mối quan hệ về hướng và độ dài của mỗi vectơ với vectơ . Viết đẳng thức thể hiện mối quan hệ giữa hai vectơ .

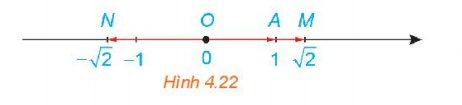
Trả lời rút gọn: 

+) và cùng hướng, và ngược hướng.

+

Bài 4: có mối quan hệ gì?

Trả lời rút gọn: 

Bài 5 : Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?

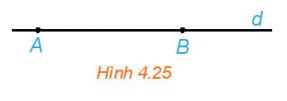
a. Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để  

b. Với điểm M bất kì, ta luôn có

c. Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t≤0 để 

Trả lời rút gọn: 

a, c đúng

2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ

Bài 1: Với ≠  và hai số thực k, t, những khẳng định nào sau đây đúng?

Trả lời rút gọn: 

a, b, c, d đúng

Bài 2: Hãy chỉ ra trên Hình 4.26 hai vectơ .Từ đó, nêu mối quan hệ giữa .

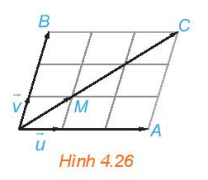
Trả lời rút gọn: 

, .

.

=> =

Bài 3: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có:

Trả lời rút gọn: 

Vì G là trọng tâm tam giác ABC nên

:

 =>

Bài 4 : Trong hình 4.27, hãy biểu thị mỗi vectơ  theo hai vectơ tức là tìm các số x, y, z, t để ;

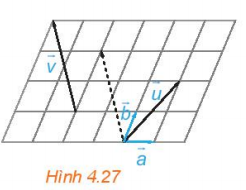
Trả lời rút gọn: 

; 

BÀI TẬP CUỐI SGK

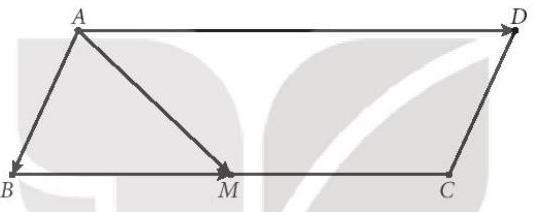
Bài 4.11: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị theo hai vectơ .

Trả lời rút gọn: 

Do là hình bình hành nên .

Do là trung điểm của nên thẳng hàng theo thứ tự đó và  => .

=> .

Bài 4.12 : Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng

Trả lời rút gọn: 

Do là trung điểm của và là trung điểm của CD, nên ta có:

(1) 

và . (2) 

và .

Cộng vế với vế của (3) và (4) ta được

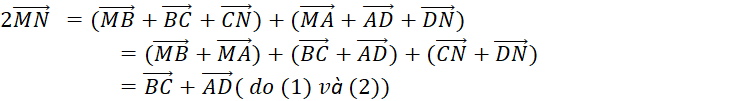
+) Tương tự, từ 

.

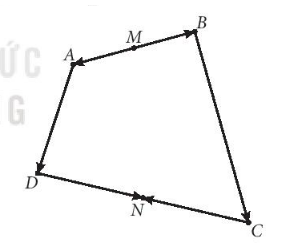
Bài 4.13: Cho hai điểm phân biệt A và B.

a. Hãy xác định điểm K sao cho

b. Chứng minh rằng với mọi điểm O, ta có

Trả lời rút gọn: 

a) Giả sử có điêm thoả mãn . Khi đó . 

=> và cùng phương, ngược hướng và  => điểm thuộc đoạn và .

b) Với điểm O bất kì, ta có:

(1) 

Và (2)

Tù (1) và (2) suy ra

=>

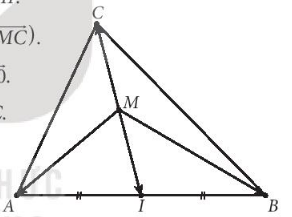
Bài 4.14 : Cho tam giác ABC

a. Hãy xác định điểm M để

b. Chứng minh rằng với mọi điểm O, ta có

Trả lời rút gọn: 

a) Giả sử có điểm thoả mãn .

Gọi là trung điểm của => .

=> .

Từ đó đẳng thức (1) tương đương với .

Điều này xảy ra ⇔ là trung điểm của .

b) Với mọi điểm  

=> .

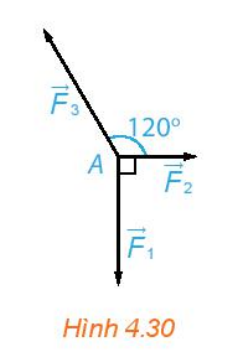
Bài 4.15 : Chất điểm A chịu tác động của ba lực như Hình 4.30 và ở trạng thái cân bằng (tức là .Tính độ lớn của các lực biết có độ lớn là 20N.

Trả lời rút gọn: 

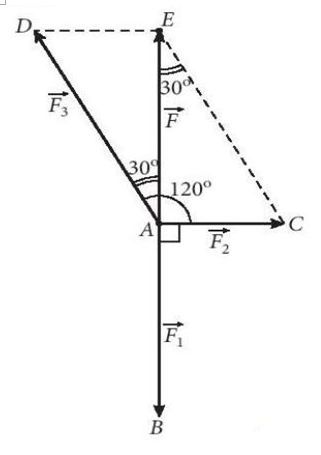
Ta dùng các vectơ để biểu diễn cho các lực tác động vào chất điểm , vectơ biểu diễn cho lực   là hợp lực của và .

=>

và  => và .

Vậy có độ lớn bằng và có độ lớn bằng .