Slide bài giảng toán 10 kết nối bài 8: Tổng và hiệu của hai vectơ

Tóm lược nội dung

BÀI 8.TỔNG VÀ HIỆU CỦA HAI VECTƠ

1. TỔNG CỦA HAI VECTƠ

Bài 1: Với hai vectơ cho trước, lấy một điểm A và vẽ các vectơ Lấy điểm A' khác A và cũng vẽ các vectơ .Hỏi hai vectơ có mối quan hệ gì?

Trả lời rút gọn: 

Bài 2: Cho hình bình hành ABCD.Tìm mối quan hệ giữa hai vectơ

Trả lời rút gọn: 

Bài 3: a. Trong Hình 4.14a, hãy chỉ ra vectơ và vectơ 

b. Trong Hình 4.14b, hãy chỉ ra vectơ và vectơ

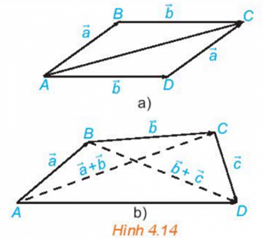
Trả lời rút gọn: 

a) 

b)

Bài 4: Cho hình thoi ABCD với cạnh có độ dài bằng 1 và . Tính độ dài của các vectơ ;

Trả lời rút gọn: 

Do ABCD là hình thoi có

=> ABC, ADC là các tam giác đều => CA = CB = CD = 1. (1)

Theo quy tắc hình bình hành, ta có:

.

.

Do tính giao hoán và tính kết hợp của phép cộng vectơ, nên:

.

2.HIỆU CỦA HAI VECTƠ

Bài 1: Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cân bằng thì hai vectơ này có mối quan hệ gì với nhau?

Trả lời rút gọn: 

Hai lực cân bằng là hai lực mạnh như nhau, có cùng phương nhưng ngược chiều, tác dụng vào cùng một vật.

Hai vectơ sẽ ngược hướng nhau, điểm đầu của vectơ này là điểm cuối của vectơ kia và có độ dài bằng nhau.

Bài 2: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng

Trả lời rút gọn: 

Do M là trung điểm của AB nên ta có:

Tương tự ta có:

Từ đó suy ra:

Bài 3: Tính lực kéo cần thiết một khẩu pháo có trọng lượng 22148 N (ứng với khối lượng xấp xỉ 2260 kg) lên một con dốc nghiêng 30^o so với phương nằm ngang. Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?

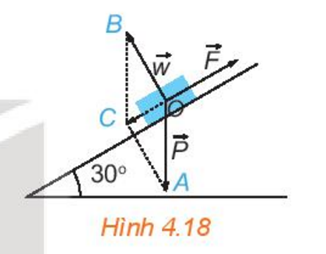
Trả lời rút gọn: 

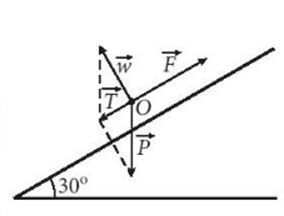
Lực tổng hợp của trọng lực và phản lực là lực theo phương dốc, hướng từ đỉnh dốc xuống chân dốc, có độ lớn ==11074 (N).

Bởi vậy, để kéo được pháo lên dốc =11074 (N).

Do nên nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu 111 người để kéo pháo lên dốc.

BÀI TẬP CUỐI SGK

Bài 4.6 : Cho bốn điểm A, B, C, D. Chứng minh rằng:

a.

b. =

Trả lời rút gọn: 

a) 

b)

Vậy =

Bài 4.7 : Cho hình bình hành ABCD. Hãy tìm điểm M  để  Tìm mối quan hệ giữa hai vectơ và

Trả lời rút gọn: 

Giả sử tìm được điểm thoả mãn .

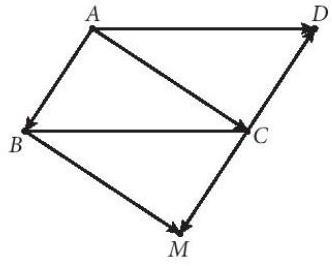
theo quy tắc hình bình hành 

 theo kết quả Bài tập 4.3,  là một hình bình hành.

Vậy điểm cần tìm là đỉnh thứ tư của hình bình hành dựng trên hai cạnh .

là hình bình hành nên . (1)

là hình bình hành nên . (2)

Từ (1) và (2) suy ra và là hai vectơ đối nhau.

Bài 4.8: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ 

Đáp án:

+)

+) Dựng hình bình hành ABDC có:

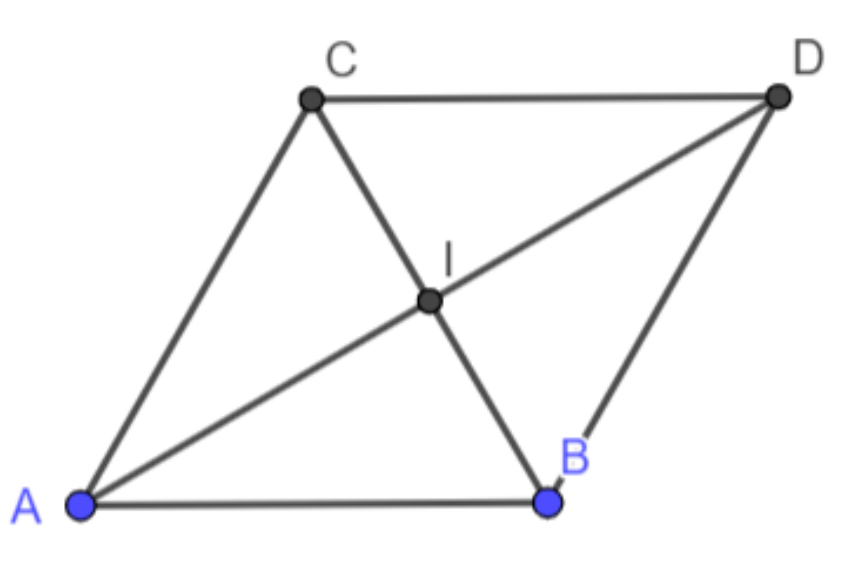
Gọi I là giao của AD và CB, AD = 2AI

Bài 4.9 :  Hình 4.19 biểu diễn hai lực cùng tác động lên một vật, cho . Tính độ lớn của hợp lực

Trả lời rút gọn: 

và .

Theo định lí côsin, ta có .

Bài 4.10 : Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn được giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Trả lời rút gọn: 

Giả sử tàu thứ nhất xuất phát từ hướng về hạ lưu và tàu thứ hai xuất phát từ hướng về thượng nguồn.

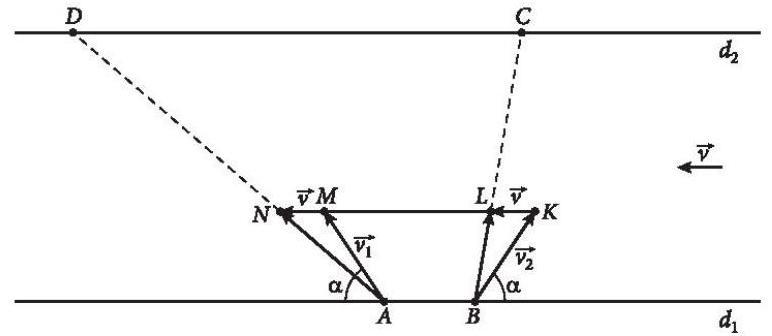
Ta sử dụng các vectơ để biểu diễn cho vận tốc của dòng nước, vận tốc riêng của tàu thứ nhất và tàu thứ hai.

Lấy các điểm sao cho .

tứ giác là một hình thang cân.

Lấy các điểm sao cho . Khi đó cùng nằm trên một đường thẳng song song với và các vectơ tương ứng biểu diễn cho vận tốc thực của tàu thứ nhất và tàu thứ hai.

Khi đó tàu thứ nhất chuyển động theo hướng đến đích là điểm và tàu thứ hai chuyển động theo hướng và đến đích là điểm bên bờ đối diện.

Do các đường thẳng đôi một song song, nên theo định lí Thales

Suy ra hai tàu cần thời gian như nhau để sang được đến bờ bên kia.

Bởi vậy cả hai tàu sang đến bờ bên kia cùng một lúc.