Từ một điểm nằm ngoài đường tròn kẻ các tiếp tuyến

1. 

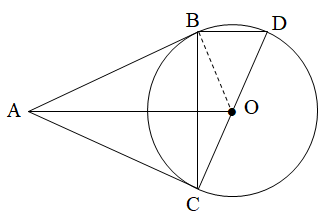
a, Ta có:

AB = AC (tính chất hai tiếp tuyến cắt nhau)

OB = OC (vì bán kính của (O)) 

=> OA là trung trực của đoạn BC nên OA $\perp $ BC (1)

b, Vì tam giác BCD có cạnh CD là đường kính của đường tròn ngoại tiếp nên tam giác BCD vuông tại B hay BC $\perp $ BD (2)

Từ (1) và (2) => OA // BD

c, Do AB tiếp xúc với (O) tại B, nên AB $\perp $ BO,

=> Tam giác ABO vuông tại B có cạnh huyền AO = 2BO = 4cm.

=> $\widehat{A}=30^{0}$, do đó $\widehat{BAC}=60^{0}$ 

Suy ra tam giác ABC là tam giác đều đồng thời $\widehat{BOA}=60^{0}$.

Trong tam giác ABO vuông tại B có cạnh AB đối diện với góc $60^{0}$ nên:

sin$60^{0}$ = $\frac{AB}{AO}$ <=> AB = AO.sin$60^{0}$ = 4.$\frac{\sqrt{3}}{2}$ = 2$\sqrt{3}$ (cm)

2.

Theo tính chất của hai tiếp tuyến cắt nhau thfi AB = AC => Tam giác ABC cân tại A.

AO là tia phân giác của góc A nên AO $\perp $ BC tại H

a, Áp dụng hệ thức về cạnh trong tam giác vuông ABO có BH là đường cao ta có:

OB$^{2}$ = OH.OA <=> 6$^{2}$ = OH.10

<=> OH = 3,6cm => AH = 10 - 3,6 = 6,4 (cm)

b, Áp dụng hệ thức về cạnh trong tam giác vuông ABO có BH là đường cao ta có:

AB$^{2}$ = HA.OA = 6,4.10 = 64 => AB = 8cm