Giải câu 3 trang 129 sách toán VNEN lớp 7 tập 1

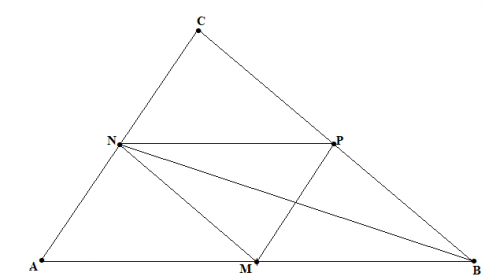
a) Xét $\bigtriangleup BMN$ và $\bigtriangleup NPB$ có:

NB chung;

$\widehat{N_{1}} = \widehat{B_{2}}$ (hai góc so le trong);

$\widehat{B_{1}} = \widehat{N_{2}}$ (hai góc so le trong).

$\Rightarrow $ $\bigtriangleup BMN = \bigtriangleup NPB$ (g.c.g).

Tương tự: $\bigtriangleup ANP = \bigtriangleup PMA$ (g.c.g).

Suy ra: AM = NP (hai cạnh tương ứng).

b) Xét $\bigtriangleup AMN$ và $\bigtriangleup NPC$ có:

AM = NP (theo câu a);

$\widehat{NAM} = \widehat{CNP}$ (hai góc đồng vị);

$\widehat{NMA} = \widehat{CPN}$ ($= \widehat{PBM}$).

$\Rightarrow $ $\bigtriangleup AMN = \bigtriangleup NPC$ (g.c.g).

Suy ra: AN = NC (hai cạnh tương ứng).