Giải câu 1 trang 127 sách toán VNEN lớp 7 tập 1

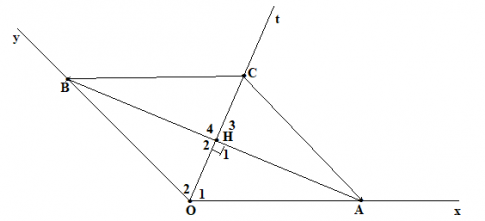
a) Xét $\bigtriangleup OHA$ và $\bigtriangleup OHB$ có:

OH cạnh chung;

$\widehat{O_{1}} = \widehat{O_{2}}$ (Ot là tia phân giác);

$\widehat{H_{1}} = \widehat{H_{2}}$;

$\Rightarrow $ $\bigtriangleup OHA = \bigtriangleup OHB$; (g.c.g)

Suy ra: HA = HB (hai cạnh tương ứng bằng nhau) hay H là trung điểm của AB.

b) Xét $\bigtriangleup HAC$ và $\bigtriangleup HBC$ có:

CH cạnh chung;

$\widehat{H_{3}} = \widehat{H_{4}}$;

HA = HB (theo câu a)

$\Rightarrow $ $\bigtriangleup HAC = \bigtriangleup HBC$ (c.g.c);

Suy ra: $\widehat{ACO} = \widehat{BCO}$ (hai góc tương ứng bằng nhau).