Bài tập về tính chất ba đường phân giác của tam giác

1. 

Xét $\Delta $BIH có $\widehat{H}=90^{\circ}$

$\Rightarrow \widehat{BIH}=90^{\circ}-\widehat{B_{2}}=90^{\circ}-\frac{\widehat{B}}{2}$ (BI là tia phân giác)    (1)

Xét $\Delta $AIC có $\widehat{DIC}$ là góc ngoài nên $\widehat{DIC}=\widehat{A_{1}}+\widehat{C_{1}}$

Mà $\widehat{A_{1}}+\widehat{C_{1}}=\frac{\widehat{A}}{2}+\frac{\widehat{C}}{2}=\frac{180^{\circ}_\widehat{B}}{2}=90^{\circ}-\frac{\widehat{B}}{2}$    (2)

Từ (1) và (2) $\Rightarrow \widehat{BIH}=\widehat{CID}$

2. 

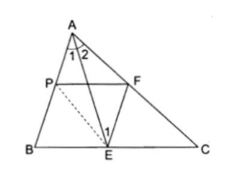
Có $\widehat{A_{1}} = \widehat{E_{1}}$ (EF // AB)

Mà $\widehat{A_{1}} = \widehat{A_{2}}$

$\Rightarrow \widehat{E_{1}} = \widehat{A_{2}}$

$\Delta $AFE có $\widehat{E_{1}} = \widehat{A_{2}}$ $\Rightarrow $ $\Delta $AFE cân tại F

$\Rightarrow $ FA = FE   (1)

Nối PF. Xét $\Delta $APF và $\Delta $EFP có:

$\widehat{APF}=\widehat{PFE}$ (AB // EF)

PE chung

$\widehat{PFA}=\widehat{FPE}$ (PE // AC)

$\Rightarrow $ $\Delta $APF = $\Delta $EFP (g.c.g)

$\Rightarrow $ AP = EF     (2)

Từ (1) và (2) suy ra AF = AP

3. 

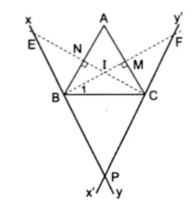
a) $\Delta $BMC có: $\widehat{M}=90^{\circ}; \widehat{C}=60^{\circ}$

$\Rightarrow \widehat{B_{1}}=30^{\circ}$

Mà $\widehat{B}=60^{\circ}$

$\Rightarrow \widehat{B_{1}}=\frac{1}{2}\widehat{B}$ nên BF là tia phân giác của góc $\widehat{B}$

Tương tự, xét $\Delta $BNC ta cũng chứng minh được CE là phân giác của $\widehat{C}$

Trong $\Delta $ABC có BM và CN là hai đường phân giác của $\widehat{B}$ và $\widehat{C}$ cắt nhau tại I. Do đó AI là phân giác của $\widehat{A}$

Vậy BF, CE, AI đồng quy.

b) Ta có:

BF $\perp $ AC

PE // AC

$\Rightarrow $ BF $\perp $ PE

Mà BF là tia phân giác của $\widehat{B}$ , trong đó $\widehat{B}$ và $\widehat{CBm}$ là góc kề bù nhau, vậy BP cũng là tia phân giác của góc $\widehat{CBm}$

Tương tự ta có CP là tia phân gíc của góc $\widehat{BCn}$

$\Delta $ABC có xy và x'y' là hai đường phân giác của hai góc ngoài $\widehat{CBm}$ và $\widehat{BCn}$. AI là tia phân giác của góc $\widehat{A}$ không kề với hai góc đó nên 3 đường AI, xy, x'y' đồng quy.

4. 

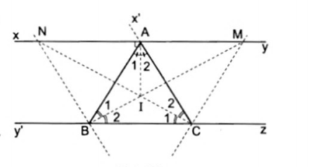
a) AI là tia phân giác góc $\widehat{A}$ mà xy $\perp $ AI vậy xy là tia phân giác của $\widehat{BAx'}$ (góc kề bù với $\widehat{A}$, tức là góc ngoài của $\Delta $ABC tại A)

N là giao điểm của đường phân giác góc $\widehat{C}$ và góc ngoài tại A. Vậy BN là tia phân giác của $\widehat{ABy'}$ (góc ngoài tại B). Suy ra BN $\perp $ BM (hai đường phân giác của hai góc kề bù nhau)

Chứng minh tương tự, ta vẽ góc ngoài tại C nên CM $\perp $ CN

b) NB là tia phân giác góc ngoài của $\widehat{B}$

CM là tia phân giác góc ngoài của $\widehat{C}$

AI là tia phân giác góc trong của $\widehat{A}$

Vậy BN, CM và AI đồng quy