Bài tập về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
1. Cho $\Delta $ABC cân tại A, kẻ AH $\perp $ BC (H thuộc BC). Trên tia đối của tia HA lấy điểm F sao cho HF = HA. Trên tia đối của tỉa CB lấy điểm E tùy ý. Chứng minh rằng:
a) AB = AC = FB = FC
b) $\Delta $AEF cân
2. Đoạn thẳng MN = 12cm; PQ = 8cm cắt nhau tại O là trung điểm của mỗi đoạn và góc tạo thành giữa 2 đoạn thẳng đó là $60^{\circ}$ ($\widehat{MOQ}=60^{\circ}$)
a) Nêu cách tìm hình chiếu của đoạn MN trên đường thẳng PQ, và cách tìm hình chiếu của đoạn PQ trên đường thẳng MN.
b) Tính độ dài của hai hình chiếu đó.
3. Cho $\Delta $ABC:
a) Từ A hạ AH $\perp $ BC (H thuộc BC). Chứng minh AH < $\frac{AB+AC}{2}$
b) Từ B hạ BK $\perp $ AC (K thuộc AC), từ C hạ CI $\perp $ AB (I thuộc AB). Chứng minh rằng : AH + BK + CI nhỏ hơn chu vi $\Delta $ABC.
4. Cho $\Delta $PMN có $\widehat{P}$ nhọn, Px là tia nằm giữa hai tia PM và PN. Kẻ MH $\perp $ Px, NK $\perp $ Px (H, K thuộc Px). Chứng minh rằng:
a) MH + NK < MN
b) Tìm vị trí của tia Px để MH + NK = MN
1.
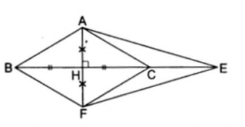
a) AB = AC (giả thiết) $\Rightarrow $ BH + HC (đường xiên bằng nhau nen hình chiếu bằng nhau)
AH = HF (giả thiết) $\Rightarrow $ AC = CF và AB = BF (hình chiếu bằng nhau nên đường xiên bằng nhau)
Do đó AB = AC = CF = BF
b) Ta có : AH = HF $\Rightarrow $ AE = EF (hình chiếu bằng nhau nên đường xiên bằng nhau)
Vậy $\Delta $AEF cân tại E.
2.
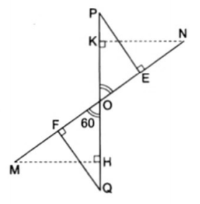
a) Muốn tìm hình chiếu của đoạn thẳng MN trên đường thẳng PQ, ta đi tìm hình chiếu của hai đầu mút đoạn thẳng đó lên PQ. Tức là từ M và N hạ các đường vuông góc với đường thẳng PQ.
Hạ MH $\perp $ PQ và NK $\perp $ PQ nên ta có HK là hình chiếu của MN trên đường thẳng PQ.
Tương tự cách tìm trên ta có EF là hình chiếu của PQ trên đường thẳng MN.
b) Chứng minh: $\Delta $HOM = $\Delta $KON (cạnh huyền - góc nhọn) $\Rightarrow $ OH = Ok..
Tương tự ta có OE = OF
Xét $\Delta $MHO có $\widehat{H}=90^{\circ}$ (theo cách vẽ); $\widehat{O}=60^{\circ}$ (giả thiết), vậy $\widehat{M}=30^{\circ}$.
OH là cạnh đối diện với góc $\widehat{M}=30^{\circ}$ nên OH = $\frac{1}{2}$OM
$\Rightarrow OH=\frac{1}{2}.\frac{12}{2}=3$ (cm)
Vậy OH = OK = 3cm, HK = 6cm
Tương tự, xét $\Delta $POE có: $\widehat{E}=90^{\circ}; \widehat{O}=60^{\circ}\Rightarrow \widehat{P}=30^{\circ}$
$\Rightarrow OE = \frac{1}{2}PO \Rightarrow OE=\frac{1}{2}.\frac{8}{2}=2$ (cm)
Vậy OE = OF = 2cm; EF = 4cm
3.
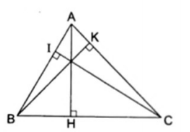
a) AH < AC (đường vuông góc nhỏ hơn đường xiên)
AH < AB (đường vuông góc nhỏ hơn đường xiên)
$\Rightarrow $ 2AH < AB + AC. Hay AH < $\frac{AB+AC}{2}$
b) Chứng minh tương tự như trên ta có:
BK < $\frac{AB+BC}{2}$
CI < $\frac{AC+BC}{2}$
Từ (1), (2) và (3) ta có:
AH + BK + CI < $\frac{AB+AC+AB+BC+AC+BC}{2}$
Hay AH + BK + CI < AB+BC+AC
4.
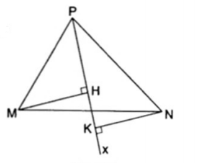
a) MH < MI; NK < IN (đường vuông góc nhỏ hơn đường xiên)
Vậy MH + NK < MI + IN (I nằm giữa hai điểm M và N)
Vậy MH + NK < MN
b) Nếu Px $\perp $ MN thì MH $\perp $ Px nên MH trùng với MN (vì qua M chỉ có một đường thẳng vuông góc với Px).
Tương tự ta có NK trùng với MN, tức là K trùng với H. Khi đó MH + KN = MN.
Vậy khi Px $\perp $ MN thì MH + KN = MN (khi đó H trùng với K)

Bình luận