Bài tập về chứng minh tứ giác nội tiếp

1.

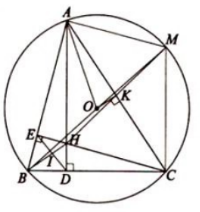
a) Vì $\widehat{AEC}=\widehat{ADC}=90^{\circ}$ nên tứ giác AEDC nội tiếp.

Theo trên, tứ giác AEDC nội tiếp nên $\widehat{BAC}=\widehat{BDI}$ (cùng bù với $\widehat{EDC}$)

Mặt khác $\widehat{BAC}=\widehat{BMC}$ (cùng chắn cung BC) suy ra $\widehat{BDI}=\widehat{BMC}$, dẫn đến tứ giác DIMC nội tiếp (đpcm)

b) Từ giả thiết BM là đường kính, ta có MA $\perp $ AB.

Lại có CH $\perp $ AB, suy ra AM // CH.

Tiếp theo, do CM $\perp $ BC, AD $\perp $ BC nên AH // CM. 

$\Rightarrow $ AHCM là hình bình hành. 

Từ đó K là trung điểm của AC.

Suy ra OK $\perp $ AC (đpcm)

c) Xét $\Delta $AKO vuông có $\widehat{AOK}=60^{\circ}$ suy ra $\widehat{OAK}=30^{\circ}$ do đó OK = $\frac{1}{2}$OA = $\frac{1}{2}$OB

Lại do OK là đường trung bình của $\Delta $BHM nên OK = $\frac{1}{2}$BH

Suy ra BH = BO, nghĩa là $\Delta $BHO cân tại B (đpcm)

2.

a) Ta thấy $\widehat{EBN}=\widehat{ECN}=45^{\circ}$

$\Rightarrow $ tứ giác BENC nội tiếp.

$\widehat{FBM}=\widehat{FAM}=45^{\circ}$

$\Rightarrow $ tứ giác BFMA nội tiếp.

b) Từ kết quả câu a, tứ giác BCNE nội tiếp nên $\widehat{BCN}+\widehat{BEN}=180^{\circ}$. Mà $\widehat{BCN}=90^{\circ}$

$\Rightarrow \widehat{BEN}=90^{\circ}$ hay $\widehat{MEN}=90^{\circ}$

Tương tự ta cũng chứng minh được $\widehat{MFN}=90^{\circ}$

Do đó tứ giác MEFN nội tiếp đường tròn đường kính MN (đpcm)

c) Từ câu b, ta thấy H là trực tâm tam giác BMN. Từ đó BI $\perp $ MN.

Có $\widehat{BNC}=\widehat{BEC}$ (cùng chắn cung BC), $\widehat{BEC}=\widehat{BNI}$ (cùng bù với $\widehat{FEM}$) nên $\widehat{BNC}=\widehat{BNI}$ 

Xét $\Delta $BCN và $\Delta $BIN là hai tam giác vuông có:

BN chung

$\widehat{BNC}=\widehat{BNI}$ 

$\Rightarrow $ $\Delta $BCN = $\Delta $BIN (cạnh huyền - góc nhọn)

$\Rightarrow $ BI = BC = a

3. 

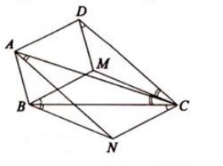
a) Vì tứ giác BMCN là hình bình hành nên $\widehat{BCN}=\widehat{CBM}$ (so le trong)

Lại theo giả thiết $\widehat{CBM}=\widehat{CDM}$, suy ra $\widehat{BCN}=\widehat{CDM}$ (1)

Ta có CN // BM; BM // AD nên CN // AD nghĩa là tứ giác ADCN là hình bình hành

$\Rightarrow $ AN // CD. Mà AB // DM

$\Rightarrow \widehat{BAN}=\widehat{MDC}$ (2) (góc có cạnh tương ứng song song)

Từ (1) và (2) suy ra $\widehat{BAN}=\widehat{BCN}$

Do đso tứ giác ABNC nội tiếp (đpcm)

b) Ta có $\widehat{BCM}=\widehat{CBN}$ (so le trong)

Vì tứ giác ABNC nội tiếp nên $\widehat{CBN}=\widehat{CAN}$ (cùng chắn cung NC)

Mặt khác $\widehat{CAN}=\widehat{ACD}$ (2 góc so le trong)

Do đó $\widehat{BCM}=\widehat{ACD}$