Bài tập chứng minh biểu thức không đổi khi một điểm di chuyển trên đường tròn
4. Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của nửa đường tròn. Qua điểm M bất kì thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến với nửa đường tròn cắt Ax, By theo thứ tự tại C và D.
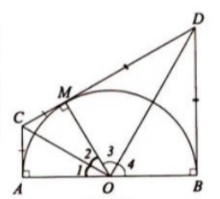
Chứng minh rằng:
a, $\widehat{COD}=90^{0}$
b, CD = AC + BD
c, Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.
Theo tính chất hai tiếp tuyến cắt nhau ta có:
a, $\left\{\begin{matrix}\widehat{O_{1}}=\widehat{O_{2}} & & \\ \widehat{O_{3}}=\widehat{O_{4}} & & \end{matrix}\right.$
=> $\widehat{AOB}=\widehat{O_{1}}+\widehat{O_{2}}+\widehat{O_{3}}+\widehat{O_{4}}$
= $2\widehat{O_{1}}+2\widehat{O_{3}}=2.(\widehat{O_{1}}+\widehat{O_{3}})=2\widehat{COD}=180^{0}$
=> $\widehat{COD}=\frac{180^{0}}{2}=90^{0}$
b, $\left\{\begin{matrix}CM=CA & & \\ DM=DB & & \end{matrix}\right.$
=> CD = CM + MD = CA + BD
c, Gọi bán kính của nửa đường tròn là R thì OM = R
Áp dụng hệ thức về đường cao cho tam giác COD vuông tại O, ta có:
OM$^{2}$ = MC.MD = AC.BD = R$^{2}$
R$^{2}$ không đổi => Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận