Trắc nghiệm đại số 10 : Ôn tập chương 1
Câu hỏi và bài tập trắc nghiệm đại số 10:Ôn tập chương I. Phần này Tech 12h sẽ giúp học sinh ôn luyện kiến thức bài học trong chương trình toán học lớp 10 ở Chương I. Với mỗi câu hỏi, các em hãy chọn đáp án của mình. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết các đáp án. Hãy bắt đầu nào!
Câu 1: Trong các mệnh đề sau mệnh đề nào đúng?
- A. $\forall x\in \mathbb{R}:x^{2}>0$
- B. $\forall n\in \mathbb{N}:4n+3$
- C. $\exists x\in \mathbb{R}:x^{2}-4x+5=0$
D. $\exists x\in \mathbb{R}:2x>x^{2}$
Câu 2: Cho mệnh đề: " Với mọi số nguyên $n$ không chia hết cho 3, $n^{2}-1$ chia hết cho 3". Mệnh đề phủ định của mệnh đề trên là mệnh đề nào dưới đây?
A. " Tồn tại số nguyên $n$ không chia hết cho 3.$n^{2}-1$ không chia hết cho 3"
- B. " Tồn tại số nguyên $n$ không chia hết cho 3, $n^{2}-1$ chia hết cho 3"
- C. " Tồn tại số nguyên $n$ chia hết cho 3, $n^{2}-1$ chia hết cho 3"
- D. " Tồn tại số nguyên $n$ chia hết cho 3, $n^{2}-1$ không chia hết cho 3"
Câu 3: Trong các câu sau, câu nào là mệnh đề đúng?
A. Nếu $a$ chia hết cho 9 thì $a$ chia hết cho 3
- B. Nếu em chăm chỉ thì em thành công
- C. Nếu một tam giác có một góc bằng $60^{\circ}$ thì tam giác đó đều
- C. Nếu $a\geq b$ thì $a^{2}\geq b^{2}$
Câu 4: Cho mệnh đề sau: "Phương trình $ax^{2}+bx+c=0$ vô nghiệm"
Mệnh đề nào dưới đây là mệnh đề phủ định của mệnh đề trên?
A. " Phương trình $ax^{2}+bx+c=0$ có nghiệm"
- B. " Phương trình $ax^{2}+bx+c=0$ có hai nghiệm phân biệt"
- C. " Phương trình $ax^{2}+bx+c=0$ có nghiệm kép"
- D. " Phương trình $ax^{2}+bx+c=0$ vô nghiệm"
Câu 5: Tập hợp $\left (-4; 3 \right ]\cap \mathbb{Z}$ bằng tập hợp nào dưới đây?
A. { -3; -2; -1; 0; 1; 2; 3 }
- B. { -4; -3; -2; -1; 0; 1; 2; 3 }
- C. { -3; -2; -1; 0; 1; 2 }
- D. { 0; 1; 2; 3 }
Câu 6: Cho
$A$ = (-3; 2);
$B= \left (0;5 \right ]$
Khi đó $A\cup B$ bằng?
- A. (0; 2)
- B. ( 2; 5)
- C. ( -3; 5)
D. $ \left (-3;5 \right ]$
Câu 7: Tính số tập con có hai phần tử của $M$ = { 1; 2; 3; 4; 5; 6 }?
- A. 18
- B. 22
C. 15
- D. 16
Câu 8: Lớp 10T có 40 học sinh, trong đó có 10 bạn học sinh giỏi Toán, 15 bạn học sinh giỏi Lý, và 22 bạn không giỏi môn nào trong hai môn Toán và Lý. Hỏi Lớp 10T có bao nhiêu bạn học sinh vừa giỏi Toán vừa giỏi Lý?
- A. 18
- B. 25
- C. 10
D. 7
Câu 9: Cho hai tập hợp
$ A= \left (-\infty ;1 \right ]$;
$B= \left \{ x\in \mathbb{R}:-3<x\leq 5 \right \}$
Tập hợp $A\cap B$ là?
- A. $\left (-3 ;1 \right ]$
- B. $\left [ 1; 5 \right ]$
C. $\left (1; 5 \right ]$
- D. $\left (-\infty ;5 \right ]$
Câu 10: Cho các tập hợp
$A= \left [ -2; +\infty \right )$
$B= \left [ 2; 5 \right )$
Hãy xác định tập hợp $A\cap B\cap C$?
- A. ( -2; 5)
- B. (2; 3)
C. $\left [ 2; 3 \right )$
- D. (1; +\infty)
Câu 11: Cho tập hợp $ A= \left \{ x\in \mathbb{R}:x^{2}+x+1=0 \right \}$.
Hãy xác định các phần tử của $A$?
- A. $A$ = {Ø}
B. $A$ = Ø
- C. $A$ = 0
- D. $A$ = {0}
Câu 12: Cho số thực $m$ > 0. Điều kiện cần và đủ để hai tập hợp $(-\infty ;\frac{1}{m})$ và $(4m; +\infty )$ có giao khác rỗng là:
- A. $0<m\leq \frac{1}{2}$
B. $0<m<\frac{1}{2}$
- C. $0<m<\frac{1}{4}$
- D. $0<m\leq \frac{1}{4}$
Câu 13: Xét hai tập hợp $A$ và $B$ và các khẳng định sau:
(I). Nếu $B\subset A$ thì $A\cap B=B$ (II). Nếu $A\subset B$ thì $A\cup B=A$
(III). $B\subset A(B\neq A)$ thì $A$ \ $B$ = Ø (IV). Nếu $A\cap B$ = Ø thì $A$ \ $B$ = $A$
Trong các khẳng định trên có bao nhiêu khẳng định là mệnh đề đúng?
- A. 1
B. 2
- C. 3
- D. 4
Câu 14: Cho tập $A= \left \{ x\in \mathbb{R}:\left | x \right | \geq 2\right \}$
Khi đó phần bù của $A$ trong $\mathbb{R}$ là?
- A. $\left [ -2; 2 \right ]$
B. $(-2; 2)$
- C. $(-\infty ; -2)\cup (2; +\infty )$
- D. $\left (-\infty; -2 \right ]\cup \left [ 2; +\infty \right )$
Câu 15: Tập hợp $\mathbb{R}$ \ $((2; 5)\cap \left [ 3; 7 \right ))$ là tập hợp nào dưới đây
- A. $\left [ 3; 5 \right )$
- B. $\left (-\infty ;2 \right ]\cup \left [ 7; +\infty \right )$
- C. $\left (-\infty ;3 \right ]\cup (5; +\infty )$
D. $(-\infty ; 3)\cup \left [ 5; + \infty \right )$
Câu 16: Cho mệnh đề chứa biến $P(m): " m\in \mathbb{Z}:2m^{2}-1 \vdots 7"$
Mệnh đề đúng là:
- A. $P(-4)$
- B. $P(-3)$
C. $P(5)$
- D. $P(6)$
Câu 17: Biểu diễn trên trục số của tập hợp là hình nào dưới đây?
- A.
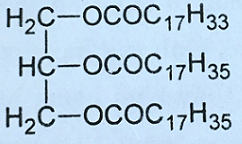
B.
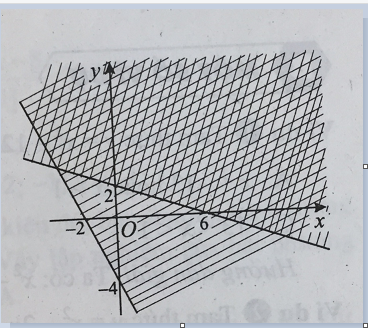
- C.

- D.
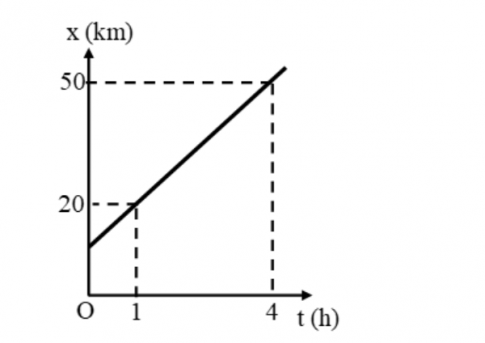
Câu 18: Một chiếc chiếu hình chữ nhật có
chiều rộng là $1,8m\pm 0,005m$,
chiều dài là $2m \pm 0,010m$.
Chu vi của chiếc chiếu đó là
- A. $7,6m\pm 0,005m$
- B. $7,6m\pm 0,010m$
- C. $7,6m\pm 0,015m$
D. $7,6m\pm 0,030m$
Câu 19: Chiều cao của di tích lịch sử Cột cờ Hà Nội do một người đo được là $\bar{h}= 41,34m\pm 0,05m$. Khi đó, số quy tròn của chiều cao $h$ = 41,34 là:
- A. 41$m$
- B. 41,4$m$
C. 41,3$m$
- D. 41,2$m$
Câu 20: Với tập $X$ có hữu hạn phần tử, kí hiệu |$X$| là số phần tử của $X$.
Cho $A,B$ là hai tập hợp hữu hạn phần tử.
Sắp xếp các số $\left | A\cup B \right |$, |$A$ \ $B$|, $ \left |A \right |+\left | B \right |$ theo thứ tự không giảm ta được:
A. |$A$ \ $B$|, $\left | A\cup B \right |, \left | A \right |+\left | B \right |$
- B. $\left | A\cup B \right |, \left | A \right |+\left | B \right |$, |$A$ \ $B$|
- C. $\left | A\cup B \right |$, |$A$ \ $B$|, $\left | A \right |+\left | B \right |$
- D. $\left | A \right |+\left | B \right |, \left | A\cup B \right |$, |$A$ \ $B$|

Bình luận