Lý thuyết trọng tâm toán 7 kết nối bài 16: Tam giác cân, đường trung trực của đoạn thẳng
Tổng hợp kiến thức trọng tâm toán 7 kết nối tri thức bài 16 Tam giác cân, đường trung trực của đoạn thẳng. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 16. TAM GIÁC CÂN. ĐƯỜNG TRUNG TRỰC CỦA ĐOẠN THẲNG
1. TAM GIÁC CÂN VÀ TÍNH CHẤT.
Định nghĩa:
Tam giác cân là tam giác có hai cạnh bằng nhau.
Ví dụ:
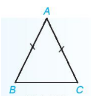
Tam giác ABC cân tại A vì AB = AC.
Hai cạnh bên: AB, AC.
Cạnh đáy: BC
Hai góc ở đáy: $\widehat{B}$,$\widehat{C}$.
Góc ở đỉnh: $\widehat{A}$.
Câu hỏi:
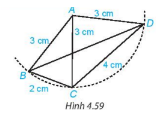
Tam giác | Cạnh bên | Cạnh đáy | Góc ở đỉnh | Góc ở đáy |
ΔABCCân tại A | AB, AC | BC | $\widehat{BAC}$ | $\widehat{ABC}$,$\widehat{ACB}$ |
ΔABDCân tại A | AB, AD | BD | $\widehat{BAD}$ | $\widehat{ABD}$,$\widehat{ADB}$ |
ΔACDCân tại A | AC, AD | CD | $\widehat{CAD}$ | $\widehat{ACD}$,$\widehat{ADC}$ |
HĐ1:

a) ΔABD=ΔACD (c.c.c) vì:
AB = AC, BD = CD, AD là cạnh chung.
b) Do đó $\widehat{B}$=$\widehat{ABD}$=$\widehat{ACD}$=$\widehat{C}$
HĐ2:

a) $\widehat{MKP}$=180$^{\circ}$-$\widehat{MPK}$-$\widehat{M}$
=180$^{\circ}$-$\widehat{NPK}$-$\widehat{N}$=$\widehat{NKP}$
b)
MPK=ΔNPK (g.c.g)
vì $\widehat{MPK}$=$\widehat{NPK}$,$\widehat{MKP}$=$\widehat{NKP}$ và PK là cạnh chung.
c) MP = NP nên tam giác MNP cân tại P.
Tính chất:
Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
GT | ΔABCcân tại A |
KL | $\widehat{ABC}$=$\widehat{ACB}$ |
GT | ΔABCcó $\widehat{ABC}$=$\widehat{ACB}$ |
KL | ΔABCcân tại A. |
Luyện tập 1:
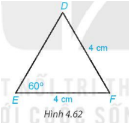
ΔDEFcân tại F, nên $\widehat{D}$=$\widehat{E}$=60$^{\circ}$.
Do đó $\widehat{F}$=180$^{\circ}$-$\widehat{D}$-$\widehat{E}$=60$^{\circ}$.
Vậy ΔDEFcũng cân tại D, do đó DE = DF = 4cm.
Nhận xét:
Tam giác DEF có các cạnh bằng nhau và các góc bằng nhau. Đó là tam giác đều.
Chú ý:
Tam giác đều là tam giác có ba cạnh bằng nhau.
Thử thách nhỏ:
a) Tam giác có ba góc bằng nhau thì cân tại một đỉnh bất kì, do đó ba cạnh bằng nhau, nên nó là tam giác đều.
b) Tam giác cân có hai góc bằng nhau, mà tổng ba góc bằng 180$^{\circ}$, lại có một góc bằng 60$^{\circ}$, nên cả ba góc bằng nhau và do đó nó là tam giác đều.
3. ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
HĐ 3:
a) O là trung điểm của đoạn AB.
b) Đường thẳng d vuông góc với AB.
Định nghĩa:
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
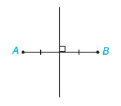
d ⊥AB
và d đi qua trung điểm I của AB
⇒d là trung trực đoạn AB
Nhận xét:
Đường trung trực của một đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
Câu hỏi:
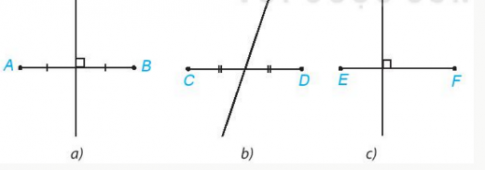
Hình a) Lan vẽ đúng.
Hình b) và c) Lan vẽ sai.
HĐ4:
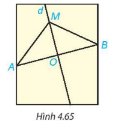
AM = BM.
Tính chất:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ (SGK – tr83)
Tính chất:
Mọi điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Luyện tập 2:

Do M nằm trên đường trung trực của đoạn AB nên MA = MB = 3 cm.
ΔMABcân tại M nên
$\widehat{MBA}$=$\widehat{MAB}$=60$^{\circ}$
Thực hành (SGK – tr 83).
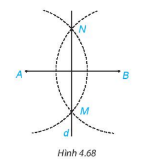
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận