Dễ hiểu giải Toán 12 Chân trời Bài 3: Ứng dụng hình học của tích phân
Giải dễ hiểu Bài 3: Ứng dụng hình học của tích phân. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Chân trời dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN
1. Tính diện tích hình phẳng
Hình phẳng giới hạn bởi đồ thị một hàm số, trục hoành và hai đường thẳng ![]() ,
, ![]()
Hoạt động 1: Gọi ![]() là đồ thị của hàm số
là đồ thị của hàm số ![]() . Kí hiệu
. Kí hiệu ![]() là diện tích hình phẳng giới hạn bởi
là diện tích hình phẳng giới hạn bởi ![]() , trục hoành và trục tung;
, trục hoành và trục tung; ![]() , là diện tích hình phẳng giới hạn bởi
, là diện tích hình phẳng giới hạn bởi ![]() , trục hoành và đường thẳng
, trục hoành và đường thẳng ![]() (Hình 1).
(Hình 1).
a) Tính ![]() , và so sánh với
, và so sánh với ![]() .
.
b) Tính ![]() , và so sánh với
, và so sánh với ![]() .
.
c) So sánh ![]() với
với ![]() .
.

Giải nhanh:
a) ![]()
b) ![]()
c) ![]()
Thực hành 1: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
Ta có:
![]() hoặc
hoặc ![]()
Với ![]() thì
thì ![]()
Với ![]() thì
thì ![]()


![]()
Thực hành 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
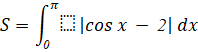
Với ![]() thì
thì ![]() (do
(do ![]() )
)

Hình phẳng giới hạn bởi đồ thị hai hàm số và hai đường thẳng ![]() ,
, ![]()
Hoạt động 2: Cho hai hàm số ![]() và
và ![]() lần lượt có đồ thị
lần lượt có đồ thị ![]() và
và ![]() như Hình 4.
như Hình 4.
a) Tính diện tích ![]() của hình phẳng giới hạn bởi
của hình phẳng giới hạn bởi ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
b) Tính diện tích ![]() của hình phẳng giới hạn bởi
của hình phẳng giới hạn bởi ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() .
.

Giải nhanh:
a) ![]()
b)

Gọi ![]() là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng ![]() và
và ![]()
![]()
Diện tích ![]() của hình phẳng giới hạn bởi
của hình phẳng giới hạn bởi ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() là:
là:
![]()
Thực hành 3: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
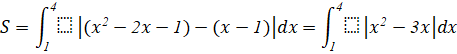
Ta có: ![]() hoặc
hoặc ![]()
Phương trình chỉ có nghiệm 1 thuộc đoạn ![]() là
là ![]()
![]()
![]()
Thực hành 4: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
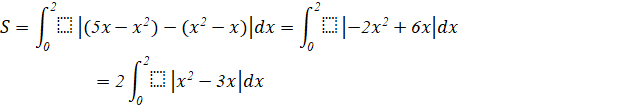
Ta có: ![]() hoặc
hoặc ![]()
Phương trình chỉ có nghiệm 1 thuộc đoạn ![]() là
là ![]()

Vận dụng 1: Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7. Tính diện tích của cửa hầm.

Giải nhanh:
Xác định trục tọa độ ![]() như hình, với
như hình, với ![]()

Phương trình của đồ thị parabol có dạng: ![]()
Vì 3 điểm ![]() thuộc đồ thị hàm số nên ta có:
thuộc đồ thị hàm số nên ta có:
![]()
![]()
![]()
=> ![]()
![]()
Như vậy, diện tích của cửa hầm là diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() và trục hoành, và bằng:
và trục hoành, và bằng:

2. Tính thể tích hình khối
Hoạt động 3: Trong không gian, cho hình chóp ![]() có đáy là hình vuông cạnh
có đáy là hình vuông cạnh ![]() ,
, ![]() ,
, ![]() . Đặt trục số
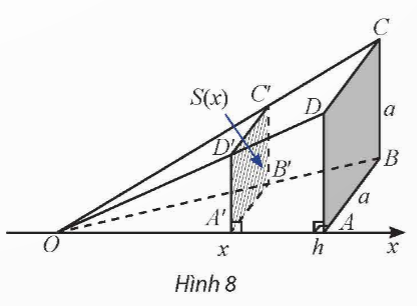
. Đặt trục số ![]() như Hình 8. Một mặt phẳng vuông góc với trục
như Hình 8. Một mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() , cắt hình chóp
, cắt hình chóp ![]() theo mặt cắt là hình vuông
theo mặt cắt là hình vuông ![]() . Kí hiệu
. Kí hiệu ![]() là diện tích của hình vuông
là diện tích của hình vuông ![]() .
.
a) Tính ![]() theo
theo ![]() ,
, ![]() và
và ![]() .
.
b) Tính ![]() và so sánh với thể tích của khối chóp
và so sánh với thể tích của khối chóp ![]() .
.
Giải nhanh:
a) Vì mặt cắt ![]() vuông góc với trục
vuông góc với trục ![]() nên
nên ![]()
Lại có ![]()
=> ![]()
Xét ![]() và
và ![]() có
có ![]()
![]()
![]() hay
hay ![]()
![]()
![]()

b) ![]()
![]()
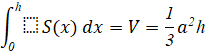
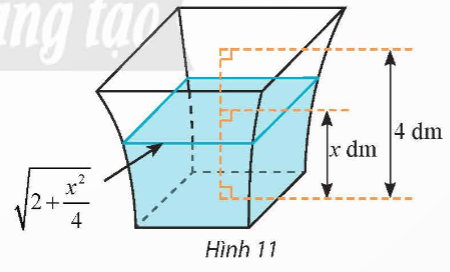
Thực hành 5: Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao ![]() (dm)
(dm) ![]() thì mặt nước là hình vuông có cạnh
thì mặt nước là hình vuông có cạnh ![]() (dm). Tính dung tích của bình.
(dm). Tính dung tích của bình.
Giải nhanh:
Chọn trục ![]() vuông góc với 2 mặt đáy của bình nước, sao cho 2 đáy bình nằm trong 2 mặt phẳng
vuông góc với 2 mặt đáy của bình nước, sao cho 2 đáy bình nằm trong 2 mặt phẳng ![]() và
và ![]()
Mặt nước vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() cắt bình nước theo mặt cắt có diện tích không đổi
cắt bình nước theo mặt cắt có diện tích không đổi ![]() .
.
![]()
![]()
![]()
Thể tích khối tròn xoay
Hoạt động 4: Cho D là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và đường thẳng
, trục hoành và đường thẳng ![]() (Hình 12a). Quay hình
(Hình 12a). Quay hình ![]() xung quanh trục
xung quanh trục ![]() thì được một khối nón, kí hiệu là
thì được một khối nón, kí hiệu là ![]() (Hình 12b).
(Hình 12b).
a) Cắt khối ![]() bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() thì mặt cắt là hình gì? Tính diện tích
thì mặt cắt là hình gì? Tính diện tích ![]() của mặt cắt đó.
của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón ![]() .
.

Giải nhanh:
a) Khi cắt khối ![]() bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() thì mặt cắt là hình tròn có bán kính bằng
thì mặt cắt là hình tròn có bán kính bằng ![]()
![]()
b) ![]()
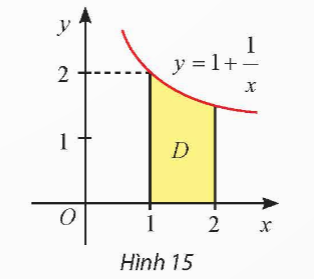
Thực hành 6: Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() (Hình 15). Tính thể tích khối tròn xoay tạo thành khi quay
(Hình 15). Tính thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục
quanh trục ![]() .
.
Giải nhanh:


Giải nhanh:
a) Khi cắt khối ![]() bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() thì mặt cắt là hình tròn có bán kính bằng
thì mặt cắt là hình tròn có bán kính bằng ![]()
![]()
b) ![]()
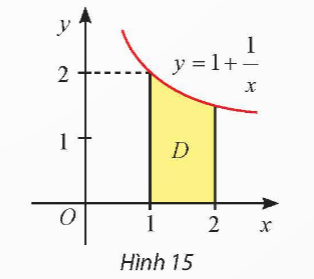
Thực hành 6: Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() (Hình 15). Tính thể tích khối tròn xoay tạo thành khi quay
(Hình 15). Tính thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục
quanh trục ![]() .
.
Giải nhanh:
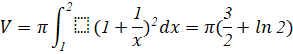
Vận dụng 2: Sử dụng tích phân, tính thể tích khối nón có bán kính đáy ![]() và chiều cao
và chiều cao ![]() (Hình 16).
(Hình 16).

Giải nhanh:
Kẻ hệ trục toạ độ ![]() như hình dưới.
như hình dưới.
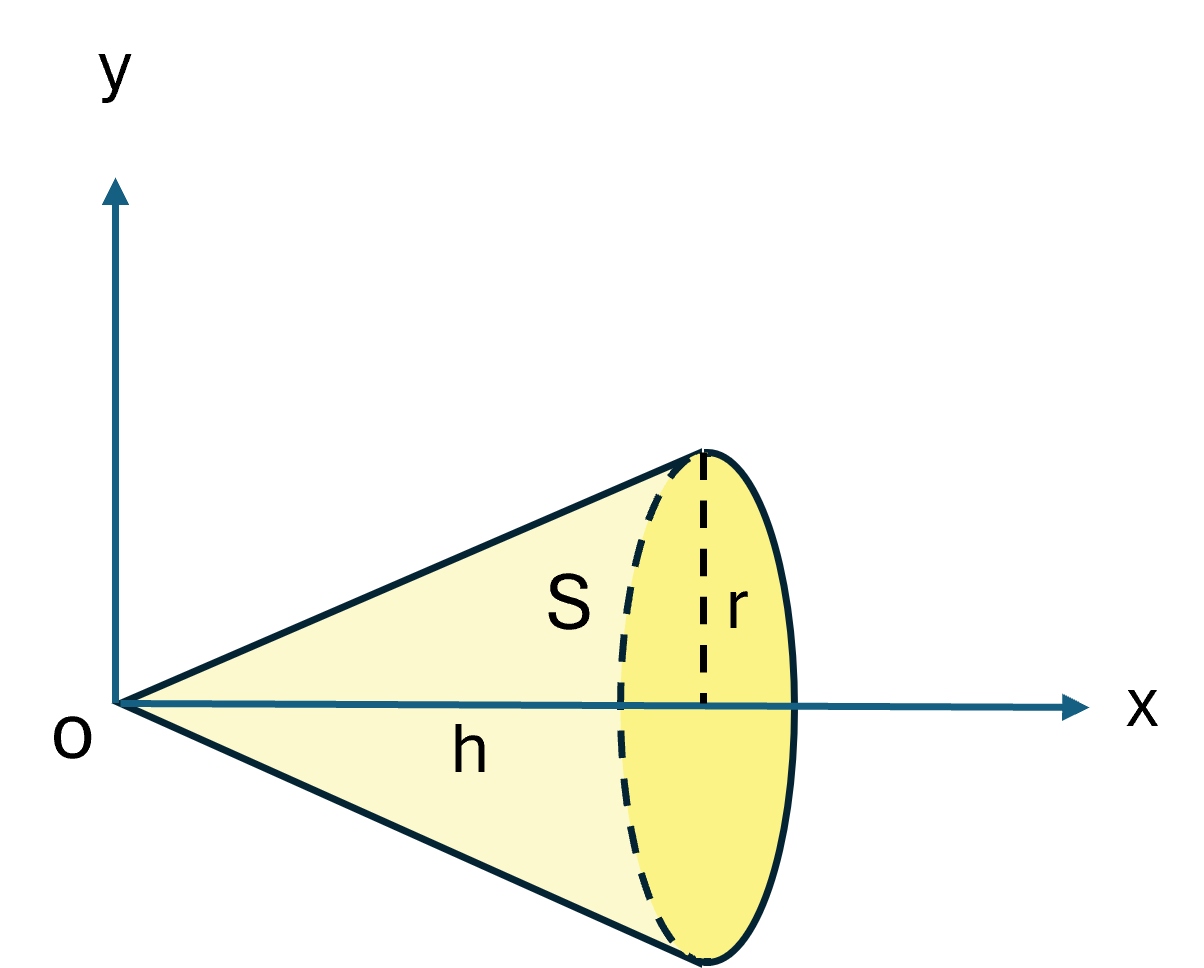
Đường thẳng ![]() đi qua 2 điểm
đi qua 2 điểm ![]() và
và ![]()
Do đó đường thẳng ![]() có phương trình:
có phương trình:
![]() hay
hay ![]()
![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và đường thẳng
, trục hoành và đường thẳng ![]() . Khi quay hình
. Khi quay hình ![]() quanh trục
quanh trục ![]() ta được một khối nón. Do đó thể tích của khối nón là:
ta được một khối nón. Do đó thể tích của khối nón là:
![]()
GIẢI BÀI TẬP
Bài 1: Tính diện tích hình phẳng giới hạn bởi
a) Đồ thị của hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
b) Đồ thị của hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
a) Diện tích hình phẳng cần tính: ![]()
Với ![]() thì
thì ![]()
Vậy ![]()
b) Diện tích hình phẳng cần tính là ![]()
Với ![]() thì
thì ![]()
![]()
![]()
Bài 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
Diện tích hình phẳng cần tính là ![]()
![]() hoặc
hoặc ![]() hoặc
hoặc ![]()
Phương trình chỉ có 2 nghiệm thuộc đoạn ![]() là
là ![]() và
và ![]()
![]()
![]()
Bài 3: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
Diện tích hình phẳng cần tính là:

Với ![]() thì
thì ![]()
![]()
![]()
Bài 4: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số ![]() ,
, ![]() và hai đường thẳng
và hai đường thẳng ![]() ,
, ![]() .
.
Giải nhanh:
Diện tích hình phẳng cần tính là ![]()
Ta có: ![]()
![]()
![]()
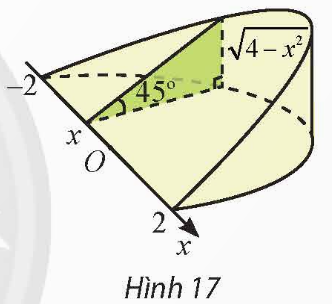
Bài 5: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() , mặt cắt là tam giác vuông có một góc 45° và độ dài một cạnh góc vuông là
, mặt cắt là tam giác vuông có một góc 45° và độ dài một cạnh góc vuông là ![]() (dm) (Hình 17). Tính thể tích của vật thể.
(dm) (Hình 17). Tính thể tích của vật thể.
Giải nhanh:
Cạnh góc vuông còn lại của tam giác vuông là: ![]()
![]()
![]()
![]()
Bài 6: Cho ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]()
![]() , trục tung và trục hoành (Hình 18). Tính thể tích khối tròn xoay tạo thành khi quay
, trục tung và trục hoành (Hình 18). Tính thể tích khối tròn xoay tạo thành khi quay ![]() quanh trục
quanh trục ![]() .
.

Giải nhanh:
![]()
![]()
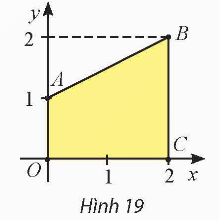
Bài 7: Trong mặt phẳng toạ độ ![]() , cho hình thang
, cho hình thang ![]() có
có ![]() ,
, ![]() và
và ![]() (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang
(Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang ![]() quanh trục
quanh trục ![]() .
.
Giải nhanh:
Đường thẳng ![]() đi qua 2 điểm
đi qua 2 điểm ![]() ,
, ![]() nên có phương trình là:
nên có phương trình là:
![]() hay
hay ![]()
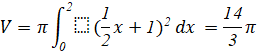
Bài 8: Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng ![]() và chiều cao bằng
và chiều cao bằng ![]() (Hình 20).
(Hình 20).

Giải nhanh:

Chọn trục ![]() sao cho gốc
sao cho gốc ![]() trùng với đỉnh của hình chóp tứ giác đều và trục đi qua tâm của đáy
trùng với đỉnh của hình chóp tứ giác đều và trục đi qua tâm của đáy
Khi đó, đáy của khối chóp nằm trên mặt phẳng vuông góc với ![]() tại
tại ![]()
Mỗi mặt vuông góc với trục ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]()
![]() , cắt hình chóp theo mặt cắt là hình vuông có diện tích
, cắt hình chóp theo mặt cắt là hình vuông có diện tích ![]()

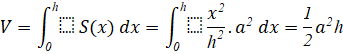
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận