TRẮC NGHIỆM

Câu 1: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.

• A.
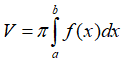
• B.
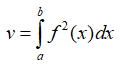
• C.

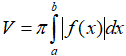
• D. 

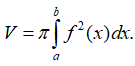
Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x³ - x và đồ thị hàm số y = x - x².

• A. 9/4

• B. 37/12

• C. 55/12
• D. 13

Câu 3: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e^2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox

• A.

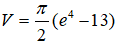
• B.

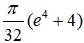
• C.
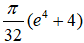
• D.  

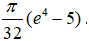
Câu 4: Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người).Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?

• A. 100 triệu     
• B. 120 triệu     

• C. 150 triệu     

• D. 250 triệu.

Câu 5: Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

• A. 1 năm     

• B. 2 năm     

• C. 3 năm     
• D. 4 năm.

Câu 6: Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng

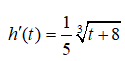
và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:

• A. 2,65cm     

• B. 2,66cm     

• C. 2,67cm     
• D. 2,68cm.

Câu 7: Thể tích khối tròn xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = lnx, y = 0, x = 2 là:

• A. π(ln²2 - 2ln2 + 1)     

• B. 2π(ln²2 - 2ln2 + 1)

• C. 4π(ln²2 - ln2 + 1)    
• D. 2π(ln²2 - ln2 + 1)

Câu 8: Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:

• A. π²     
• B. 2π²     

• C. 4π²     

• D. 8π²

Câu 9: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và cách nhau một khoảng bằng 4m. Phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản tương ứng là 150.000 đồng/m² và 100.000 đồng/m². Hỏi số tiền cần để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó gần nhất với số nào sau đây?

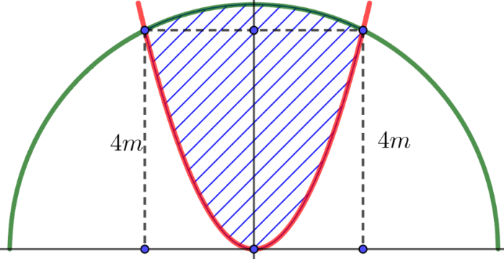
• A. 3.739.000 (đồng).

• B. 1.948.000 (đồng).
• C. 3.926.000 (đồng).
• D. 4.115.000 (đồng).

Câu 10: Ông An có một mảnh đất nhỏ hình vuông cạnh bằng 4m ở trước sân. Ông muốn trồng hoa và cỏ để trang trí mảnh vườn của mình như sau: Ông sẽ trồng hoa trên phần diện tích có dạng Parabol (P) nhận trục đối xứng KI của hình vuông làm trục đối xứng của (P) và đỉnh của (P) là trung điểm của KI như hình vẽ, phần cỏ sẽ trồng ở phần còn lại của hình vuông. Biết rằng loại hoa ông muốn trồng có giá 200.000 đồng/1m², cỏ có giá 50.000 đồng/1m². Hỏi số tiền ông An bỏ ra để làm mảnh vườn là bao nhiêu (số tiền được làm tròn đến hàng đơn vị)?

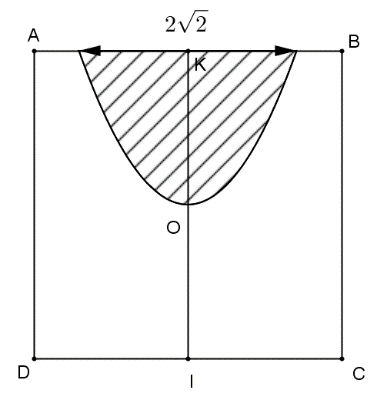
• A. 1365685,4 đ.

• B. 2634314,6 đ.
• C. 138642,5 đ.
• D. 1457847,9 đ.