BÀI TẬP CUỐI CHƯƠNG VI

CÂU HỎI TRẮC NGHIỆM

Chọn phương án đúng:

Bài 1 trang 80 toán 12 tập 2 ctst

Cho hai biến cố A và B có P(A) = 0,8;P(B) = 0,5 và P(AB) = 0,2.

a) Xác suất của biến cố A với điều kiện B là

A. 0,4. 

B. 0,5. 

C. 0,25.

D. 0,625

b) Xác suất biến cố B không xảy ra với điều kiện biến cố A xảy ra là

A. 0,6. 

B. 0,5. 

C. 0,75. 

D. 0,25

c) Giá trị của biểu thức:

là:

A. –0,5. 

B. 0. 

C. 0,5. 

D. 1.

Giải nhanh:

a) Đáp án A.

b) Đáp án C.

c) Đáp án B. 

Bài 2 trang 80 toán 12 tập 2 ctst

 Một nhà máy thực hiện khảo sát toàn bộ công nhân về sự hài lòng của họ về điều kiện làm việc tại phân xưởng. Kết quả khảo sát như sau: 

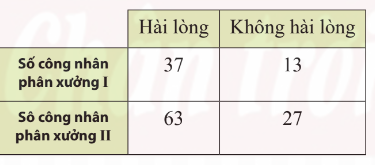
Gặp ngẫu nhiên một công nhân của nhà máy. Gọi A là biến cố “Công nhân đó làm việc tại phân xưởng I” và B là biến cố “Công nhân đó hài lòng với điều kiện làm việc tại phân xưởng”.

a) Xác suất của biến cố A là:

A.

B.

C.

D.

b) Xác suất của biến cố A với điều kiện B là:

A. 0,37.

 B. 0,5. 

C.

D.

c) Xác suất của biến cố B với điều kiện A không xảy ra là

A.

B. 0,9. 

C. 0,7. 

D.

Giải nhanh:

a) Đáp án C

b) Đáp án A.

c) Đáp án C

Bài 3 trang 80 toán 12 tập 2 ctst

 Cho sơ đồ hình cây dưới đây:

a) Xác suất của biến cố cả A và B đều không xảy ra là

A. 0,32. 

B. 0,4. 

C. 0,8. 

D. 0,92.

b) Xác suất của biến cố B là:

A. 0,42. 

B. 0,62. 

C. 0,28. 

D. 0,48.

c) Xác suất điều kiện P(A|B) là:

A.

B. 0,7

C.

D. 0,48

d) Giá trị của biểu thức:

là:

A. 0,48.

 B. 0,3. 

C. 0,5. 

D. 0,6.

Giải nhanh:

a) Đáp án A

b) Đáp án B

 c) Đáp án A.

d) Đáp án D.

BÀI TẬP TỰ LUẬN

Bài 4 trang 81 toán 12 tập 2 ctst

Một khu dân cư có 85% các hộ gia đình sử dụng điện để đun nấu. Hơn nữa, có 21% các hộ gia đình sử dụng bếp từ để đun nấu. Chọn ngẫu nhiên một hộ gia đình, tính xác suất hộ đó sử dụng bếp từ để đun nấu, biết hộ đó sử dụng điện để đun nấu.

Giải nhanh:

A  là biến cố "hộ gia đình sử dụng điện để đun nấu"

B  là biến cố "hộ gia đình sử dụng bếp từ để đun nấu".

P(A) = 0.85  (85% các hộ gia đình sử dụng điện để đun nấu)

P(B) = 0.21  (21% các hộ gia đình sử dụng bếp từ để đun nấu)

Xác suất hộ gia đình được chọn sử dụng bếp từ để đun nấu, biết hộ đó sử dụng điện để đun nấu là xác suất có điều kiện  P(B|A):

Coi tất cả các hộ gia đình sử dụng bếp từ đều sử dụng điện (bởi vì bếp từ chỉ sử dụng điện). Do đó, P(B|A) = P(B) .

Vậy xác suất một hộ gia đình sử dụng bếp từ để đun nấu, biết rằng hộ đó sử dụng điện để đun nấu, là khoảng 24.7%

Bài 5 trang 81 toán 12 tập 2 ctst

Cho 2 biến cố ngẫu nhiên A và B. Biết rằng P(A|B)=2P(B|A) và

Tính tỷ số

Giải nhanh:

 P(A|B) = 2P(B|A) 

Thay vào công thức, ta có:

=>

Bài 6 trang 81 toán 12 tập 2 ctst

Phòng công nghệ của một công ty có 4 kĩ sư và 6 kĩ thuật viên. Chọn ra ngẫu nhiên đồng thời 3 người từ phòng. Tính xác suất để cả 3 người được chọn đều là kĩ sư, biết rằng trong 3 người được chọn có ít nhất 2 kĩ sư.

Giải nhanh:

A  là biến cố "cả 3 người được chọn đều là kĩ sư"

B  là biến cố "trong 3 người được chọn có ít nhất 2 kĩ sư". 

Chúng ta cần tính xác suất P(A|B):

Vì  A  (cả 3 người được chọn đều là kĩ sư) là một trường hợp đặc biệt của  B  (có ít nhất 2 kĩ sư trong 3 người được chọn), nên  . Do đó, ta có:

P(A)  là xác suất để cả 3 người được chọn đều là kĩ sư.

Số cách chọn 3 kĩ sư từ 4 kĩ sư là 

Tổng số cách chọn 3 người từ 10 người là  .

P(B) là xác suất để trong 3 người được chọn có ít nhất 2 kĩ sư.

- Số cách chọn 2 kĩ sư từ 4 kĩ sư và 1 kĩ thuật viên từ 6 kĩ thuật viên là 

- Số cách chọn 3 kĩ sư từ 4 kĩ sư đã tính là 4

Tổng số cách thỏa mãn biến cố B  là  36 + 4 = 40 

Vậy xác suất để cả 3 người được chọn đều là kĩ sư, biết rằng trong 3 người được chọn có ít nhất 2 kĩ sư, là  

Bài 7 trang 81 toán 12 tập 2 ctst

Có hai cái hộp giống nhau, hộp thứ nhất chứa 5 quả bóng bàn màu trắng và 3 quả bóng bàn màu vàng, hộp thứ hai chứa 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Minh lấy ra ngẫu nhiên 1 quả bóng từ hộp thứ nhất. Nếu quả bóng đó là bóng vàng thì Minh lấy ra ngẫu nhiên đồng thời 2 quả bóng từ hộp thứ hai, còn nếu quả bóng đó màu trắng thì Minh lấy ra ngẫu nhiên đồng thời 3 quả bóng từ hộp thứ hai.

a) Sử dụng sơ đồ hình cây, tính xác suất để có đúng 1 quả bóng màu vàng trong các quả bóng lấy ra từ hộp thứ hai.

b) Biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng. Tính xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng.

Giải nhanh:

Ta có sơ đồ hình cây sau:

a) Xác suất lấy được đúng 1 quả bóng màu vàng: có 2 khả năng để lấy được đúng 1 quả bóng màu vàng. Xác suất này bằng tổng 2 xác suất: Lấy được 2 quả trắng 1 quả vàng và lấy được 1 quả trắng 1 quả vàng

b) Biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng, tính xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng:

Ký hiệu  W  là sự kiện lấy ra quả bóng màu trắng từ hộp thứ nhất, và  B  là sự kiện lấy ra quả bóng màu vàng từ hộp thứ nhất.

Trường hợp 1: Quả bóng từ hộp thứ nhất là màu trắng (5/8):

Trường hợp 2: Quả bóng từ hộp thứ nhất là màu vàng (3/8):

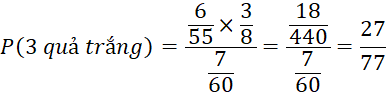
Vậy xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng khi biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng là 

Bài 8 trang 81 toán 12 tập 2 ctst

Hộp thứ nhất có 1 viên bi xanh và 5 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 5 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 2 viên bi từ hộp thứ hai.

a) Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.

b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ. Tính xác suất để 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.

Giải nhanh:

a) 

Khả năng chuyển bi từ hộp thứ nhất sang thứ hai:

- Hộp 1: 1 viên xanh, 5 viên đỏ (tổng cộng 6 viên).

- Hộp 2: 3 viên xanh, 5 viên đỏ (tổng cộng 8 viên).

Các khả năng khi chuyển 2 viên từ hộp 1 sang hộp 2:

Chuyển 2 viên đỏ: xác suất  

2. Chuyển 1 viên đỏ và 1 viên xanh: xác suất  

3. Chuyển 2 viên xanh: không thể xảy ra vì chỉ có 1 viên xanh.

Xác định số bi trong hộp thứ hai sau khi chuyển:

- Nếu chuyển 2 viên đỏ: hộp 2 có 3 xanh + 7 đỏ = 10 viên.

- Nếu chuyển 1 xanh và 1 đỏ: hộp 2 có 4 xanh + 6 đỏ = 10 viên.

Tính xác suất lấy ra 2 viên đỏ từ hộp 2

- Nếu chuyển 2 viên đỏ: xác suất lấy 2 viên đỏ là

- Nếu chuyển 1 xanh và 1 đỏ: xác suất lấy 2 viên đỏ là

Vậy xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ:

b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ. Tính xác suất để 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.

A: 2 viên bi lấy ra từ hộp thứ hai là bi đỏ

B: 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ

Xác suất để hai viên lấy từ hộp thứ hai là đỏ:

Xác suất 2 viên lấy từ hộp 1 là đỏ và sau đó lấy 2 viên đỏ từ hộp 2: 

Như vậy xác suất để 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ, biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ, là  .

Bài 9 trang 81 toán 12 tập 2 ctst

Một doanh nghiệp có 45% nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 7% và 5%. Gặp ngẫu nhiên một nhân viên của doanh nghiệp.

a) Tính xác suất nhân viên đó có mua bảo hiểm nhân thọ.

b) Biết rằng nhân viên đó có mua bảo hiểm nhân thọ. Tính xác suất nhân viên đó là nam.

Giải nhanh:

a) 

-  F  là sự kiện nhân viên đó là nữ.

-  M  là sự kiện nhân viên đó là nam.

-  I  là sự kiện nhân viên đó mua bảo hiểm nhân thọ.

-  P(F) = 45% = 0.45 

-  P(M) = 55% = 0.55  (vì P(M) = 1 - P(F) )

-  P(I|F) = 7% = 0.07  (xác suất nhân viên nữ mua bảo hiểm)

-  P(I|M) = 5% = 0.05  (xác suất nhân viên nam mua bảo hiểm)

Xác suất nhân viên mua bảo hiểm nhân thọ là:

Vậy xác suất nhân viên mua bảo hiểm nhân thọ là 5.9%.

b) Xác suất nhân viên là nam, biết rằng nhân viên đó có mua bảo hiểm nhân thọ

Vậy xác suất nhân viên đó là nam, biết rằng họ đã mua bảo hiểm nhân thọ, là khoảng 46.61%.