BÀI 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ

1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

Thực hành 1 trang 7 toán 12 tập 1 ctst

Tìm các khoảng đơn điệu của hàm số có đồ thị cho ở Hình 3. 

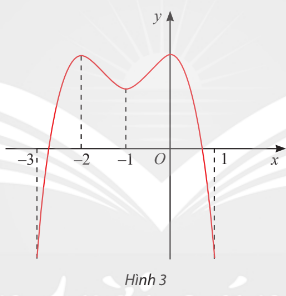
Giải nhanh:

Hàm số đồng biến trên các khoảng và

Hàm số nghịch biến trên khoảng và .

Hoạt động 1 trang 7 toán 12 tập 1 ctst

Cho hàm số 

a) Từ đồ thị hàm số (Hình 4), hãy chỉ ra các khoảng đồng biến và nghịch biến của hàm số đã cho. 

b) Tính đạo hàm và xét dấu .

c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến, nghịch biến của hàm số với dấu của .

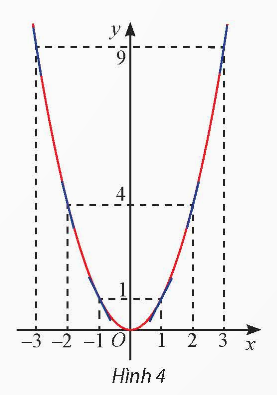
Giải nhanh:

a) Hàm số đồng biến trên khoảng từ và nghịch biến trên khoảng từ .

b) ;

Bảng biến thiên:

c) Hàm số đồng biến trên khoảng mà dương, nghịch biến trên khoảng mà âm. 

Thực hành 2 trang 9 toán 12 tập 1 ctst

Xét tính đơn điệu của các hàm số sau: 

a);                                  

b)

Giải nhanh:

a) Tập xác định:

Ta có:

hoặc (thỏa mãn)

Bảng biến thiên: 

Hàm số đồng biến trên các khoảng và ; nghịch biến trên các khoảng

b) Tập xác định:

Ta có

Vì với mọi nên với mọi

Hàm số nghịch biến trên khoảng

Thực hành 3 trang 9 toán 12 tập 1 ctst

Chứng minh hàm số đồng biến trên .

Giải nhanh:

Xét hàm số  

Tập xác định:

Ta có:

Lại có:

với mọi

Vậy hàm số đồng biến trên .

Vận dụng 1 trang 9 toán 12 tập 1 ctst

Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số với .

Giải nhanh:

Tập xác định:

Ta có:

hoặc (thỏa mãn)

Bảng biến thiên:

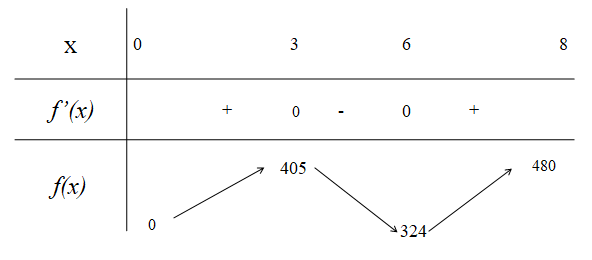
Trong thời gian từ lúc xuất phát đến thời điểm 3 phút, độ cao của khinh khí cầu tăng dần từ lên . Độ cao của khinh khí cầu tăng dần từ lên trong thời gian từ 6 phút đến 8 phút. Độ cao của khinh khí cầu giảm dần từ xuống trong thời gian từ 3 phút đến 6 phút. 

2. CỰC TRỊ CỦA HÀM SỐ

Hoạt động 2 trang 10 toán 12 tập 1 ctst

Quan sát đồ thị của hàm số trong Hình 5 

a) Tìm khoảng chứa điểm mà trên đó với mọi

b) Tìm khoảng chứa điểm mà trên đó với mọi

c) Tồn tại hay không khoảng chứa điểm mà trên đó với mọi hoặc với mọi

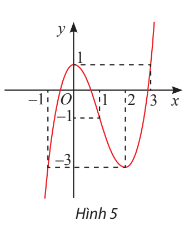
Giải nhanh:

a) Trong khoảng

b) Trong khoảng

c) Không tồn tại khoảng  

Thực hành 4 trang 11 toán 12 tập 1 ctst

Tìm các điểm cực trị của hàm số có đồ thị cho ở Hình 8. 

Giải nhanh:

là điểm cực đại 

là điểm cực tiểu 

là điểm cực tiểu 

Hoạt động 3 trang 11 toán 12 tập 1 ctst

Đồ thị của hàm số được cho ở Hình 9.

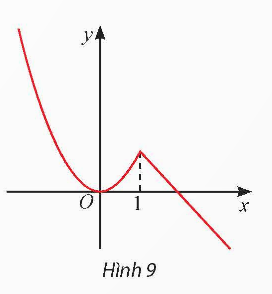
a) Tìm điểm cực đại và cực tiểu của hàm số. 

b) Tại , hàm số có đạo hàm không? 

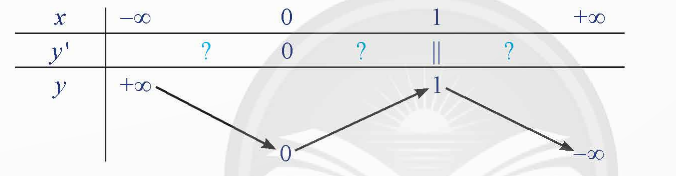
c) Thay mỗi dấu ? bằng kí hiệu thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu khi x đi qua điểm cực đại và điểm cực tiểu. 

Giải nhanh:

a) Hàm số y = f(x) có: 

là điểm cực đại vì với mọi

là điểm cực tiểu vì với mọi

b) Tại , hàm số không có đạo hàm 

c) Bảng biến thiên: 

Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì đổi dấu.

Thực hành 5 trang 12 toán 12 tập 1 ctst

Tìm cực trị của hàm số

Giải nhanh:

Xét hàm số

Tập xác định:

Ta có

hoặc (thỏa mãn)

Bảng biến thiên:

Hàm số đạt cực tiểu tại , ; hàm số cực đại tại ,

Vận dụng 2 trang 12 toán 12 tập 1 ctst

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số với

Tìm tọa độ các đỉnh của lát cắt dãy núi trên đoạn  

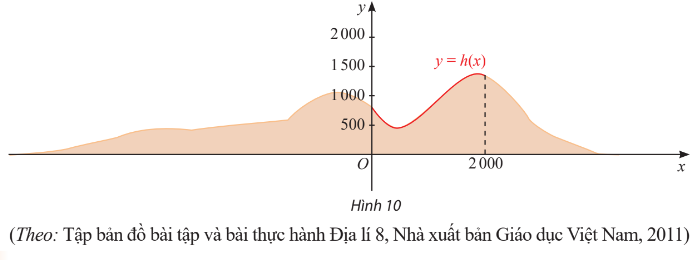
Giải nhanh:

Xét hàm số

Tập xác định:

Ta có:

hoặc (thỏa mãn)

Bảng biến thiên:

Tọa độ đỉnh cực tiểu của dãy núi là

Tọa độ đỉnh cực đại của dãy núi là

3. Bài TẬP CUỐI SÁCH GIÁO KHOA

Bài 1 trang 13 toán 12 tập 1 ctst

Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11. 

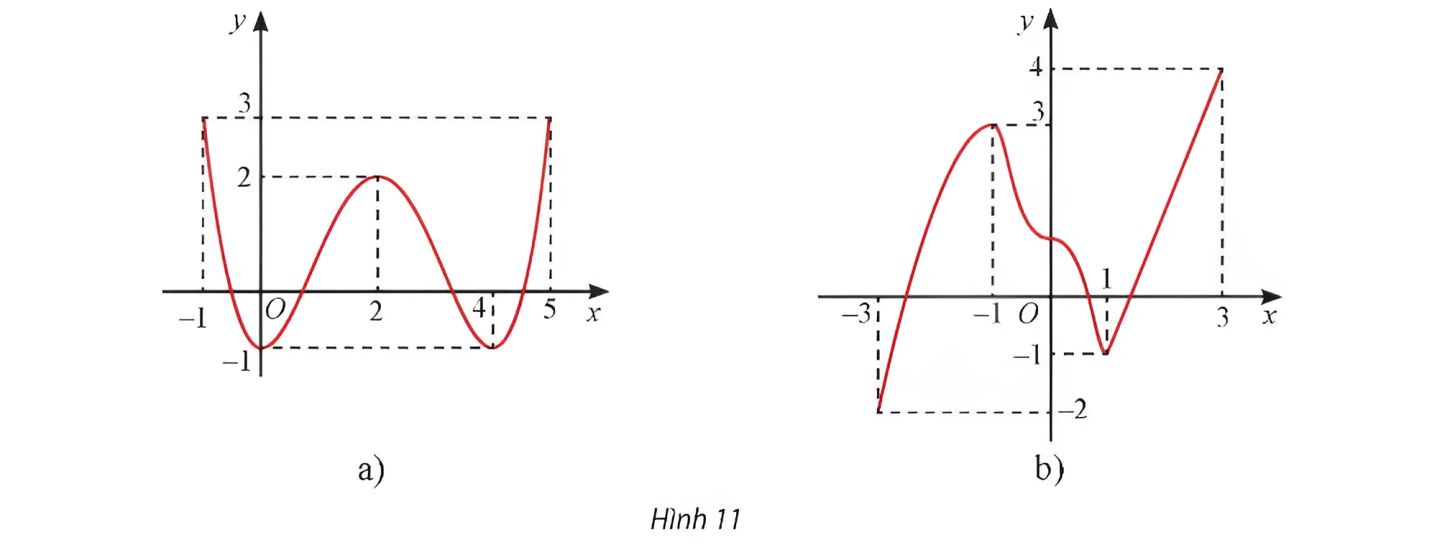
Giải nhanh:

a) Hàm số đồng biến trên các khoảng và nghịch biến trên các khoảng và  

Hàm số đạt cực tiểu tại và với ; hàm số đạt cực đại tại , với

b) Hàm số đồng biến trên các khoảng và ; nghịch biến trên các khoảng  

Hàm số đạt cực tiểu tại với ; hàm số đạt cực đại tại với

Bài 2 trang 13 toán 12 tập 1 ctst

Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: 

a) ;                       

b) . 

Giải nhanh:

a) Tập xác định:  

Ta có:

hoặc   

Bảng biến thiên: 

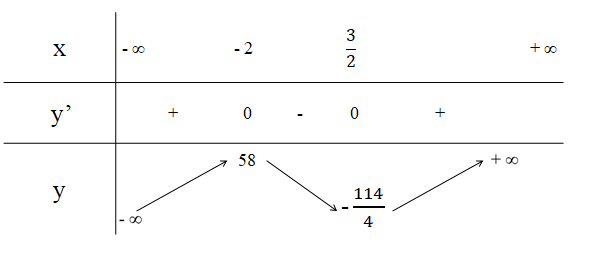
Hàm số đồng biến trên các khoảng và ; hàm số nghịch biến trên các khoảng    

Hàm số đạt cực tiểu tại với; hàm số cực đại tại với .

b) Tập xác định:

Ta có: = 

Vì với mọi nên 

Bảng biến thiên: 

Hàm số đồng biến trên các khoảng

Hàm số không có cực trị. 

Bài 3 trang 13 toán 12 tập 1 ctst

Tìm cực trị của các hàm số sau:

a) ;

b) ;

c) . 

Giải nhanh:

a) Tập xác định:  

Ta có:

hoặc

Bảng biến thiên: 

Hàm số đạt cực tiểu tại , giá trị cực tiểu là ; hàm số cực đại tại , giá trị cực đại là .

b) Xét hàm số  

Tập xác định:

Ta có:  

Vì nên   

Bảng biến thiên: 

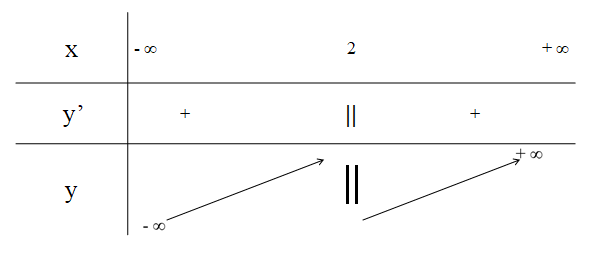
Hàm số không có cực trị. 

c) Tập xác định:

Ta có:

(thỏa mãn)

Bảng biến thiên: 

Hàm số đạt cực đại tại , giá trị cực đại . 

Bài 4 trang 13 toán 12 tập 1 ctst

Chứng minh hàm số nghịch biến trên từng khoảng xác định của nó. 

Giải nhanh:

Tập xác định:

Ta có:

Vìnên

Vậy hàm số nghịch biến trên

Bài 5 trang 13 toán 12 tập 1 ctst

Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức  (tỉ USD) với x là số năm tính từ 2010 đến 2017

a) Tính đạo hàm của hàm số .

b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Giải nhanh:

a)

b) Ta có: 

Do đó luôn đồng biến với

Vậy kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Bài 6 trang 13 toán 12 tập 1 ctst

Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số với . Khi đó là vận tốc của chất điểm tại thời điểm , kí hiệu là gia tốc chuyển động của chất điểm tại thời điểm , kí hiệu là . 

a) Tìm các hàm và .

b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Giải nhanh:

a) Ta có:

b) Tập xác định:

Bảng biến thiên: 

Vậy thì vận tốc của chất điểm giảm, từ trở đi thì vận tốc của chất điểm tăng.

Bài 7 trang 13 toán 12 tập 1 ctst

Đạo hàm của hàm số có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số .

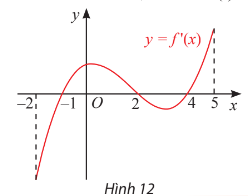
Giải nhanh:

hoặc hoặc

khi

khi

Hàm số đồng biến trên các khoảng và và nghịch biến trên các khoảng và  

Hàm số đạt cực tiểu tại và ; hàm số đạt cực đại tại .