BÀI 1. NGUYÊN HÀM

1. Khái niệm nguyên hàm

Hoạt động 1 trang 6 toán 12 tập 2 ctst 

Cho hàm số xác định trên . Tìm một hàm số sao cho .

Giải nhanh:

=

Hoạt động 2 trang 6 toán 12 tập 2 ctst 

Cho hàm số xác định trên .

a) Chứng minh rằng là một nguyên hàm của trên .

b) Với là hằng số tuỳ ý, hàm số có là nguyên hàm của trên không?

c) Giả sử là một nguyên hàm của trên . Tìm đạo hàm của hàm số . Từ đó, có nhận xét gì về hàm số ?

Giải nhanh:

a) với mọi thuộc .

=> là một nguyên hàm của hàm số trên

b)

với mọi thuộc .

Như vậy là một nguyên hàm của hàm số trên

c) Vì là một nguyên hàm của trên nên

Như vậy đạo hàm của hàm số bằng

=> Hàm số là một hằng số

Thực hành 1 trang 7 toán 12 tập 2 ctst 

Chứng minh rằng là một nguyên hàm của hàm số trên .

Giải nhanh:

với mọi thuộc

=> là một nguyên hàm của hàm số trên

2. Nguyên hàm của một số hàm sơ cấp

Nguyên hàm của hàm số lũy thừa

Hoạt động 3 trang 8 toán 12 tập 2 ctst 

 a) Giải thích tại sao và .

b) Tìm đạo hàm của hàm số . Từ đó, tìm .

Giải nhanh:

a) Vì nên là một nguyên hàm của

=> .

Vì với mọi thuộc nên là một nguyên hàm của trên

=>

b)

Vì với mọi thuộc nên là một nguyên hàm của trên

Thực hành 2 trang 8 toán 12 tập 2 ctst 

Tìm:

a)

b)

c)

Giải nhanh:

a)

b)

c)

Nguyên hàm của hàm số

Hoạt động 4 trang 8 toán 12 tập 2 ctst 

Cho hàm số với .

a) Tìm đạo hàm của .

b) Từ đó, tìm .

Giải nhanh:

a) với

b)

Nguyên hàm của một số hàm số lượng giác

Hoạt động 5 trang 9 toán 12 tập 2 ctst 

 a) Tìm đạo hàm của các hàm số , , , .

b) Từ đó, tìm , , , .

Giải nhanh:

a)  , , , .

b) 

, 

, 

, 

.

Thực hành 3 trang 9 toán 12 tập 2 ctst 

 Tìm nguyên hàm của hàm số thoả mãn

Giải nhanh:

Với ta có:

Với ta có:

Nguyên hàm của hàm số mũ

Hoạt động 6 trang 9 toán 12 tập 2 ctst 

 a) Tìm đạo hàm của các hàm số , với .

b) Từ đó, tìm và ().

Giải nhanh:

a) , ()

b) ; 

().

Thực hành 4 trang 9 toán 12 tập 2 ctst 

 Tìm:

a)

b)

Giải nhanh:

a)

b)

3. Tính chất cơ bản của nguyên hàm

Nguyên hàm của tích một số với một hàm số

Hoạt động 7 trang 10 toán 12 tập 2 ctst 

Ta có và .

a) Tìm và .

b) Tìm .

c) Từ các kết quả trên, giải thích tại sao .

Giải nhanh:

a) .

b)

c) Theo kết quả câu a) và b) ta có và đều có dạng với là một hằng số tuỳ ý.

 .

Thực hành 5 trang 10 toán 12 tập 2 ctst 

 Tìm:

a) ;

b) .

Giải nhanh:

a)

b)

Nguyên hàm của tổng, hiệu hai hàm số

Hoạt động 8 trang 10 toán 12 tập 2 ctst 

  Ta có , và

a) Tìm , và .

b) Tìm .

c) Từ các kết quả trên, giải thích tại sao .

Giải nhanh:

a)

b)

c) = với là một hằng số tuỳ ý

Thực hành 6 trang 11 toán 12 tập 2 ctst 

 Tìm:

a) ;

b) .

Giải nhanh:

a)

b)

Thực hành 7 trang 11 toán 12 tập 2 ctst 

Một ô tô đang chạy với tốc độ 19 m/s thì hãm phanh và chuyển động chậm dần với tốc độ (m/s). Kể từ khi hãm phanh, quãng đường ô tô đi được sau 1 giây, 2 giây, 3 giây là bao nhiêu?

Giải nhanh:

Gọi là quãng đường vật đi được sau hãm phanh giây

Chọn mốc thời gian là kể từ khi hãm phanh nên m/s

Vì với mọi nên: 

(m)

(m)

(m)

GIẢI BÀI TẬP

Bài 1 trang 11 toán 12 tập 2 ctst 

Tính đạo hàm của hàm số , suy ra nguyên hàm của hàm số .

Giải nhanh:

Vì với mọi nên là một nguyên hàm của

.

Bài 2 trang 11 toán 12 tập 2 ctst 

Tìm:

a) ;

b) ;

c) ;

d) .

Giải nhanh:

a)

b)

c)

d)

Bài 3 trang 11 toán 12 tập 2 ctst 

Tìm nguyên hàm của hàm số thoả mãn .

Giải nhanh:

với thì

Bài 4 trang 11 toán 12 tập 2 ctst 

Tìm:

a) ;

b) ;

c) ;

d) .

Giải nhanh:

a)

b)

c)

d)

Bài 5 trang 12 toán 12 tập 2 ctst 

Tìm:

a) ;

b) ;

c) ;

d) .

Giải nhanh:

a)

b)

c)

d)

Bài 6 trang 12 toán 12 tập 2 ctst 

Kí hiệu là chiều cao của một cây (tính theo mét) sau khi trồng năm. Biết rằng sau năm đầu tiên cây cao 2 m. Trong 10 năm tiếp theo, cây phát triển với tốc độ (m/năm). 

a) Xác định chiều cao của cây sau năm .

b) Sau bao nhiêu năm cây cao 3 m?

Giải nhanh:

a) Gọi là chiều cao của cây sau năm

Vì sau năm đầu tiên cây cao 2 m nên

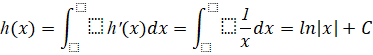
Mà

Như vậy,  

b) Cây cao 3 m (năm)

Bài 7 trang 12 toán 12 tập 2 ctst 

Một chiếc xe đang chuyển động với tốc độ = 10 m/s thì tăng tốc với gia tốc không đổi =2 . Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc.

Giải nhanh:

Kí hiệu là tốc độ của xe, là quãng đường xe đó đi được sau t giây tăng tốc

Do chọn mốc thời gian tính từ lúc xe bắt đầu tăng tốc nên

Vì với mọi nên:

= 10 m/s nên

(m/s)

Vì với mọi nên: 

Mà

(m)