BÀI TẬP CUỐI CHƯƠNG III

CÂU HỎI TRẮC NGHIỆM 

Câu 1 trang 84 toán 12 tập 1 ctst

Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là

A. 1,5.                  B. 0,9.                  C. 0,6.                  D. 0,3.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

A. 0,9.                  B. 0,975.               C. 0,5.                  D. 0,575.

c) Phương sai của mẫu số liệu ghép nhóm là

A. 3,39.                B. 11,62.               C. 0,1314.             D. 0,36.

d) Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A. 3,41.                B. 11,62.               C. 0,017.               D. 0,36.

Giải nhanh:

a) A. 1,5

b) D. 0,575

c) C. 0,1314

d) D. 0,36.

Câu 2 trang 84 toán 12 tập 1 ctst

Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi được thống kê lại ở bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là

A. 25.                   B. 20.                   C. 15.                   D. 30.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

A. 23,75.              B. 27,5.                C. 31,88.               D. 8,125.

c) Phương sai của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A. 31,77.              B. 32.                   C. 31.                   D. 31,44.

Giải nhanh:

a) A. 25

b) D. 8,125

c) D. 31,44

Câu 3 trang 85 toán 12 tập 1 ctst

Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik 3×3, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm nhận giá trị nào trong các giá trị dưới đây?

A. 6.                     B. 8.                     C. 10.                   D. 12.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

A. 10,75.              B. 1,75.                C. 3,63.                D. 14,38.

c) Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

A. 5,98.                B. 6.                     C. 2,44.                D. 2,5.

Giải nhanh:

a) C. 10                

b) C. 3,63

c) A. 5,98

BÀI TẬP TỰ LUẬN

Câu 4 trang 85 toán 12 tập 1 ctst

Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

Hãy xác định khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên. 

Giải nhanh:

Khoảng biến thiên của mẫu số liệu ghép nhóm là: (km)

Cỡ mẫu n = 30.

Gọi là mẫu số liệu gốc gồm độ dài quãng đường bác tài xế đã lái xe mỗi ngày trong một tháng và được xếp theo thứ tự không giảm.

Ta có:

;; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . 

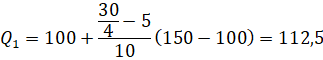
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

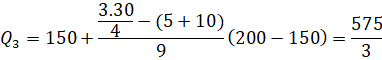
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

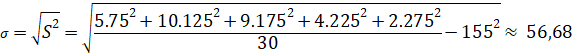
Câu 5 trang 85 toán 12 tập 1 ctst

Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh hoạ ở biểu đồ sau.

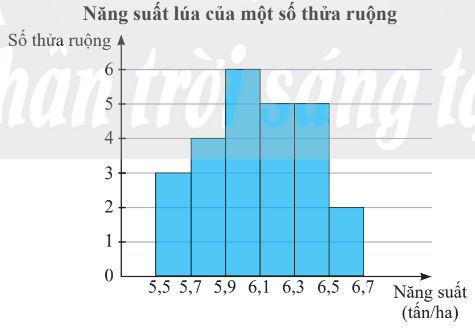
a) Có bao nhiêu thửa ruộng đã được khảo sát?

b) Lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm tương ứng của mẫu số liệu trên. 

c) Hãy xác định khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.

Giải nhanh:

a) Số thửa ruộng đã được khảo sát là:

b) 

c) Khoảng biến thiên của mẫu số liệu ghép nhóm là: (tấn/ha)

Cỡ mẫu n = 25

Gọi là mẫu số liệu gốc gồm năng suất của 25 thửa ruộng và được xếp theo thứ tự không giảm.

Ta có:

; ; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . 

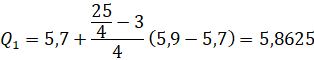
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

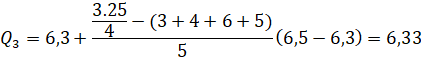
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

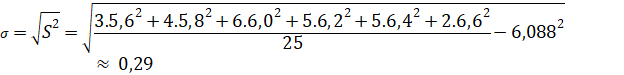
Câu 6 trang 86 toán 12 tập 1 ctst

Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau:

a) Nếu so sánh theo số trung bình thì học sinh trường nào viết nhanh hơn? 

b) Nếu so sánh theo khoảng tứ phân vị thì học sinh trường nào có tốc độ viết đồng đều hơn? 

c) Nếu so sánh theo độ lệch chuẩn thì học sinh trường nào có tốc độ viết đồng đều hơn?

Giải nhanh:

Cỡ mẫu n = 50.

a)

Vậy nếu so sánh theo số trung bình thì học sinh trường Y viết nhanh hơn.

b) Gọi là mẫu số liệu gốc gồm thời gian hoàn thành một bài viết chính tả của 50 học sinh lớp 4 trường X và được xếp theo thứ tự không giảm.

Ta có:

; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . 

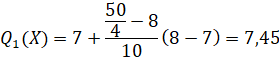
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

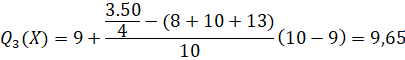
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Gọi là mẫu số liệu gốc gồm thời gian hoàn thành một bài viết chính tả của 50 học sinh lớp 4 trường Y và được xếp theo thứ tự không giảm.

Ta có: 

; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là .

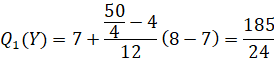
Tứ phân vị thứ ba của mẫu số liệu gốc là .

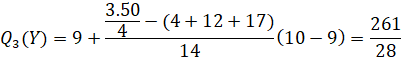
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Vậy nếu so sánh theo khoảng tứ phân vị thì học sinh trường Y có tốc độ viết đồng đều hơn

c)

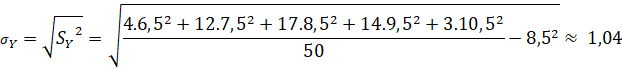
Vậy nếu so sánh theo độ lệch chuẩn thì học sinh trường Y có tốc độ viết đồng đều hơn

Câu 7 trang 86 toán 12 tập 1 ctst

Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm quan trắc đặt ở Nha Trang và Quy Nhơn.

(Nguồn: Tổng cục Thống kê)

a) Nếu so sánh theo khoảng tứ phân vị thì số giờ nắng trong tháng 6 của địa phương nào đồng đều hơn?

b) Nếu so sánh theo độ lệch chuẩn thì số giờ nắng trong tháng 6 của địa phương nào đồng đều hơn?

Giải nhanh:

Cỡ mẫu: n = 20

a) Gọi là mẫu số liệu gốc gồm tổng số giờ nắng trong tháng 6 của 20 năm tại trạm quan trắc đặt ở Nha Trang và được xếp theo thứ tự không giảm.

Ta có:

; ; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . 

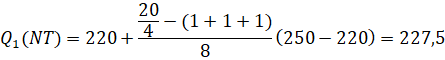
Tứ phân vị thứ ba của mẫu số liệu gốc là .

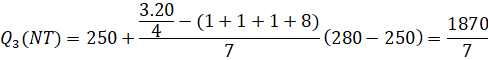
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Gọi là mẫu số liệu gốc gồm  tổng số giờ nắng trong tháng 6 của 20 năm tại trạm quan trắc đặt ở Quy Nhơn và được xếp theo thứ tự không giảm.

Ta có ; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

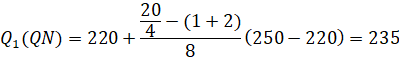
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

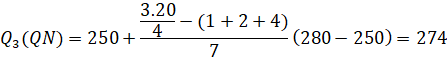
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Vậy nếu so sánh theo khoảng tứ phân vị thì số giờ nắng trong tháng 6 của Quy Nhơn đồng đều hơn

b)

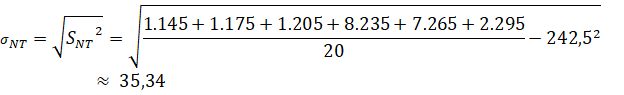
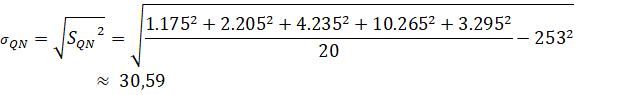
Vậy nếu so sánh theo độ lệch chuẩn thì số giờ nắng trong tháng 6 của Quy Nhơn đồng đều hơn

Câu 8 trang 86 toán 12 tập 1 ctst

Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B.

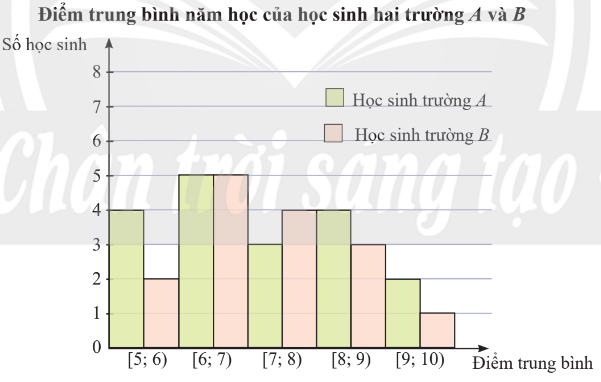
a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên.

b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?

c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?

Giải nhanh:

a) 

b) Cỡ mẫu: ;

Gọi là mẫu số liệu gốc gồm điểm trung bình của học sinh trường A và được xếp theo thứ tự không giảm.

Ta có ; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . 

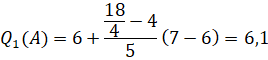
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

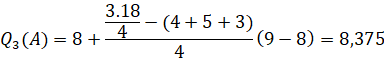
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Gọi là mẫu số liệu gốc gồm điểm trung bình của học sinh trường B và được xếp theo thứ tự không giảm.

Ta có ; ; ; ; .

Tứ phân vị thứ nhất của mẫu số liệu gốc là . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

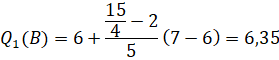
Tứ phân vị thứ ba của mẫu số liệu gốc là . 

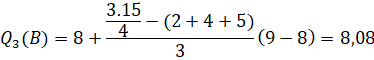
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: 

Vậy nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn

b) Số trung bình của mẫu số liệu: 

Trường A

Trường B 

Độ lệch chuẩn 

Trường A

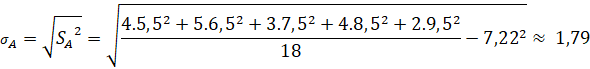
Trường B 

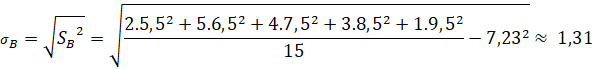
Vậy nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn