BÀI 1: Xác suất có điều kiện:

1. Xác suất có điều kiện:

Hoạt động 1 trang 69 toán 12 tập 2 ctst

Hộp thứ nhất chứa 2 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 2 viên bi xanh và

3 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Bạn Thanh lấy ra ngẫu nhiên

1 viên bi từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó lại lấy ra ngẫu nhiên 1 viên bi từ

hộp thứ hai.

Gọi A là biến cố “Viên bi lấy ra lần thứ nhất là bi xanh”;

B là biến cố “Viên bi lấy ra lần thứ hai là bi đỏ”.

a) Biết rằng biến cố A xảy ra, tính xác suất của biến cố B.

b) Biết rằng biến cố A không xảy ra, tính xác suất của biến cố B.

Giải nhanh:

a) Do hộp 1 chứa 3 viên bi bao gồm 2 bi xanh và 1 bi đỏ.

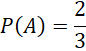
Nếu biến cố A xảy ra, hộp thứ nhất còn lại 1 bi xanh và 1 bi đỏ, hộp thứ 2 có 3 bi xanh và 3 bi đỏ.

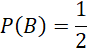
b)

Nếu biến cố A không xảy ra, hộp 1 còn lại 2 bi xanh, hộp 2 có 2 bi xanh và 4 bi đỏ.

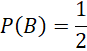
Thực hành 1 trang 70 toán 12 tập 2 ctst

 Xét phép thử lấy thẻ ở Ví dụ 1. Gọi D là biến cố “Thẻ lấy ra lần thứ hai ghi số lớn hơn 1”.

Tính P(D|A) và P(D|B).

Giải nhanh:

Biến cố D: Thẻ có số lớn hơn 1: {2, 3}.

Nếu A xảy ra, tức là thẻ lấy ra lần thứ nhất là số 1:

Số các thẻ còn lại = 2, các thẻ còn lại là 2 và 3

Xác suất lấy thẻ có số lớn hơn 1 khi đã biết thẻ đầu tiên là số 1:

Nếu B xảy ra, số thẻ lấy ra là số 2

Các thẻ còn lại là thẻ 1 và thẻ 3

Xác suất lấy thẻ lớn hơn 1:

Thực hành 2 trang 70 toán 12 tập 2 ctst 

Xét phép thử ở Ví dụ 2. Tính xác suất thành viên được chọn không biết chơi cờ tướng,

biết rằng thành viên đó biết chơi cờ vua.

Giải nhanh:

A: Biến cố "Thành viên được chọn biết chơi cờ tướng".

B: Biến cố "Thành viên được chọn biết chơi cờ vua".

: Biến cố “Thành viên được chọn không biết chơi cờ tướng”

Tổng số thành viên biết chơi cờ vua: 25

Số thành viên biết chơi cờ vua và biết chơi cờ tướng: 10

Số thành viên biết chơi cờ vua nhưng không biết chơi cờ tướng: 25−10=15

Xác suất chọn được thành viên biết chơi cờ vua nhưng không biết chơi cờ tướng là:

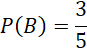
Như vậy xác suất thành viên được chọn không biết chơi cờ tướng, biết rằng thành viên đó biết chơi cờ vua là

Vận dụng 1 trang 70 toán 12 tập 2 ctst

Tính xác suất có điều kiện ở hoạt động khởi động 1(trang 70).

Giải nhanh:

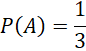
2. Công thức xác suất có điều kiện

Giải chi tiết hoạt động 2 trang 71 toán 12 tập 2 ctst

Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Gọi

A là biến cố “Xuất hiện hai mặt có cùng số chấm”, B là

biến cố “Tổng số chấm của hai mặt xuất hiện bằng 8” và

C là biến cố “Xuất hiện ít nhất một mặt có 6 chấm”.

a) Tính và P(A|B).

b) Tính và P(C|A).

Giải nhanh:

a) 

-  A : Xuất hiện hai mặt có cùng số chấm.

-  B : Tổng số chấm của hai mặt xuất hiện bằng 8.

Biến cố  B  xảy ra khi tổng số chấm của hai mặt xuất hiện bằng 8. Các cặp số chấm thỏa mãn điều kiện này là:

- (2, 6)

- (3, 5)

- (4, 4)

- (5, 3)

- (6, 2)

Vậy có 5 cặp số chấm thỏa mãn. Tổng số kết quả có thể xảy ra khi gieo hai con xúc xắc là  .

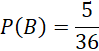
Biến cố   xảy ra khi hai mặt có cùng số chấm và tổng số chấm là 8. Duy nhất cặp (4, 4) thỏa mãn điều kiện này.

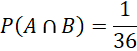
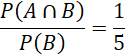
 Có 1 cặp kết quả thỏa mãn A trong 5 cặp kết quả của B. Xác suất biến cố P(A|B)

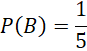
b)

-  C : Xuất hiện ít nhất một mặt có 6 chấm.

Biến cố  A  xảy ra khi hai mặt có cùng số chấm. Các cặp số chấm thỏa mãn điều kiện này là:

- (1, 1)

- (2, 2)

- (3, 3)

- (4, 4)

- (5, 5)

- (6, 6)

Có 6 cặp số chấm thỏa mãn trên 36 cặp kết quả.

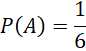
Biến cố   xảy ra khi hai mặt có cùng số chấm và ít nhất một mặt có 6 chấm. Duy nhất cặp (6, 6) thỏa mãn điều kiện này.

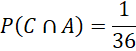
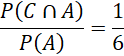
Xác suất biến cố P(C|A) là xác suất mà biến cố A thỏa mãn biến cố C. Có 1 cặp biến cố thỏa mãn:

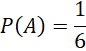
Thực hành 3 trang 72 toán 12 tập 2 ctst

Một nhóm 5 học sinh nam và 4 học sinh nữ tham gia lao động trên sân trường. Cô giáo chọn ngẫu nhiên đồng thời 2 bạn trong nhóm đi tưới cây. Tính xác suất để hai bạn được chọn có cùng giới tính, biết rằng có ít nhất 1 bạn nam được chọn.

Giải nhanh:

- A: Có ít nhất một bạn nam được chọn.

- B: Hai bạn được chọn có cùng giới tính.

Biến cố A xảy ra khi có ít nhất một bạn nam được chọn. 

Số cách chọn 2 học sinh từ 4 học sinh nữ (không có bạn nam nào) là:

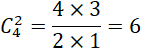
Tổng số cách chọn 2 học sinh từ 9 học sinh là:

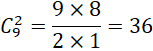
Do đó, xác suất (không có bạn nam nào được chọn) là:

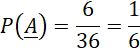
Xác suất P(A) (có ít nhất một bạn nam được chọn) là:

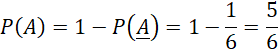
Biến cố xảy ra khi hai bạn được chọn có cùng giới tính và có ít nhất một bạn nam 

Số cách chọn 2 học sinh từ 5 học sinh nam là:

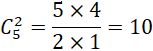
Tổng số kết quả có thể xảy ra khi chọn 2 học sinh từ 9 học sinh là:

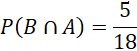
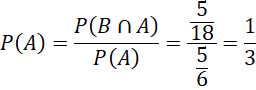
Vậy xác suất để hai bạn được chọn có cùng giới tính, biết rằng có ít nhất một bạn nam được chọn, là   

Vận dụng 2 trang 72 toán 12 tập 2 ctst

Kết quả khảo sát những bệnh nhân bị tai nạn xe máy về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:

– Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 80%;

– Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90%;

– Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu là 18%.

Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách sẽ làm giảm khả năng bị chấn thương vùng đầu bao nhiêu lần?

Giải nhanh:

- A là bệnh nhân bị chấn thương vùng đầu.

- B là bệnh nhân đội mũ bảo hiểm đúng cách.

- P(A) = 0.8  (tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn).

- P(B) = 0.9  (tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn).

-  (tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu)

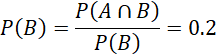
Điều này có nghĩa là khả năng bị chấn thương vùng đầu khi đội mũ bảo hiểm đúng cách là 0.2, hay nói cách khác, làm giảm khả năng bị chấn thương vùng đầu là 5 lần.

3. Sơ đồ hình cây

Hoạt động 3 trang 72 toán 12 tập 2 ctst

Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật.

Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy

ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau

vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7.

Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:

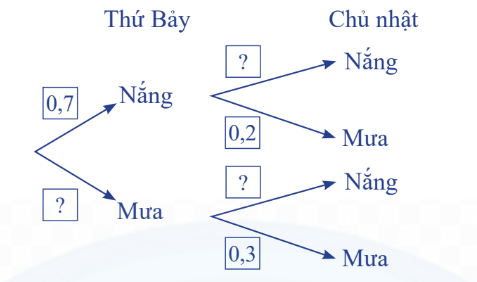
Giải nhanh:

A: Trời nắng vào thứ Bảy

B: Trời mưa vào Chủ Nhật

Dựa vào sơ đồ, ta có:

Xác suất trời mưa vào thứ Bảy:

Xác suất trời nắng vào Chủ Nhật:

Thực hành 4 trang 74 toán 12 tập 2 ctst

Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

A: “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”;

B: “Hai viên bi lấy ra có cùng màu”.

Giải nhanh:

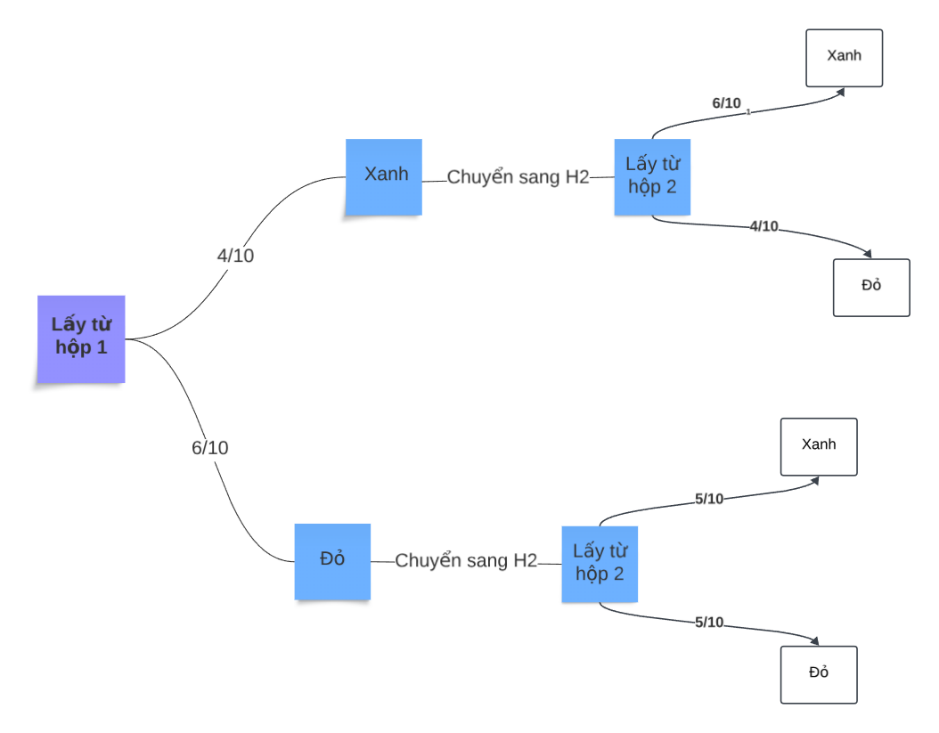
A: “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”;

B: “Hai viên bi lấy ra có cùng màu”.

Xác suất viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ là

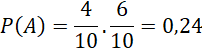
Xác suất hai viên bi lấy ra có cùng màu:

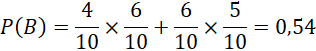
Vận dụng 3 trang 74 toán 12 tập 2 ctst 

Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là 85% đối với sinh viên tốt nghiệp loại giỏi và 70% đối với sinh viên tốt nghiệp loại khác. Tỉ lệ sinh viên tốt nghiệp loại giỏi là 30%. Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

C: “Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”;

D: “Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.

Giải nhanh:

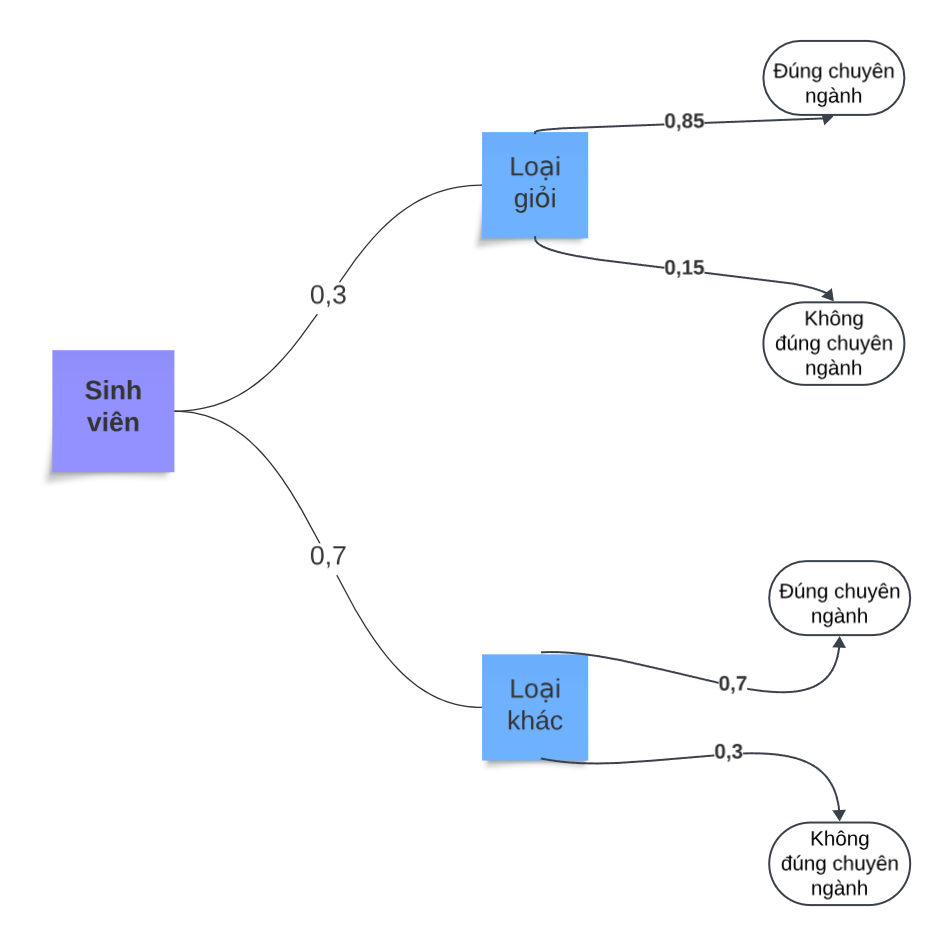
Xác suất tìm được sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành:

Xác suất của sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành:

BÀI TẬP CUỐI SÁCH GIÁO KHOA

Bài 1 trang 75 toán 12 tập 2 ctst

Một thư viện có 35% tổng số sách là sách khoa học, 14% tổng số sách là sách khoa học tự nhiên. Chọn ngẫu nhiên một quyển sách của thư viện. Tính xác suất để quyển sách được chọn là sách khoa học tự nhiên, biết rằng đó là quyển sách về khoa học.

Giải nhanh:

A: biến cố lấy được sách khoa học tự nhiên

B: biến cố lấy được sách khoa học

Có 35% là sách khoa học: P(B)=0,35

14% trong số đó là sách khoa học tự nhiên:

Xác suất để quyển sách được chọn là sách khoa học tự nhiên, biết rằng đó là quyển sách về khoa học là:

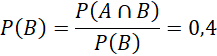
Bài 2 trang 75 toán 12 tập 2 ctst

Cho hai biến cố A và B có P(A) = 0,4; P(B) = 0,8 và. Tính và P(A|B)

Giải nhanh:

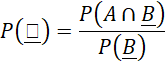
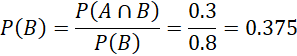
Bài 3 trang 75 toán 12 tập 2 ctst

Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7. Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

A: “Bạn được chọn là nam và học tiếng Nhật”;

B: “Bạn được chọn là nữ và học tiếng Anh”.

Giải nhanh:

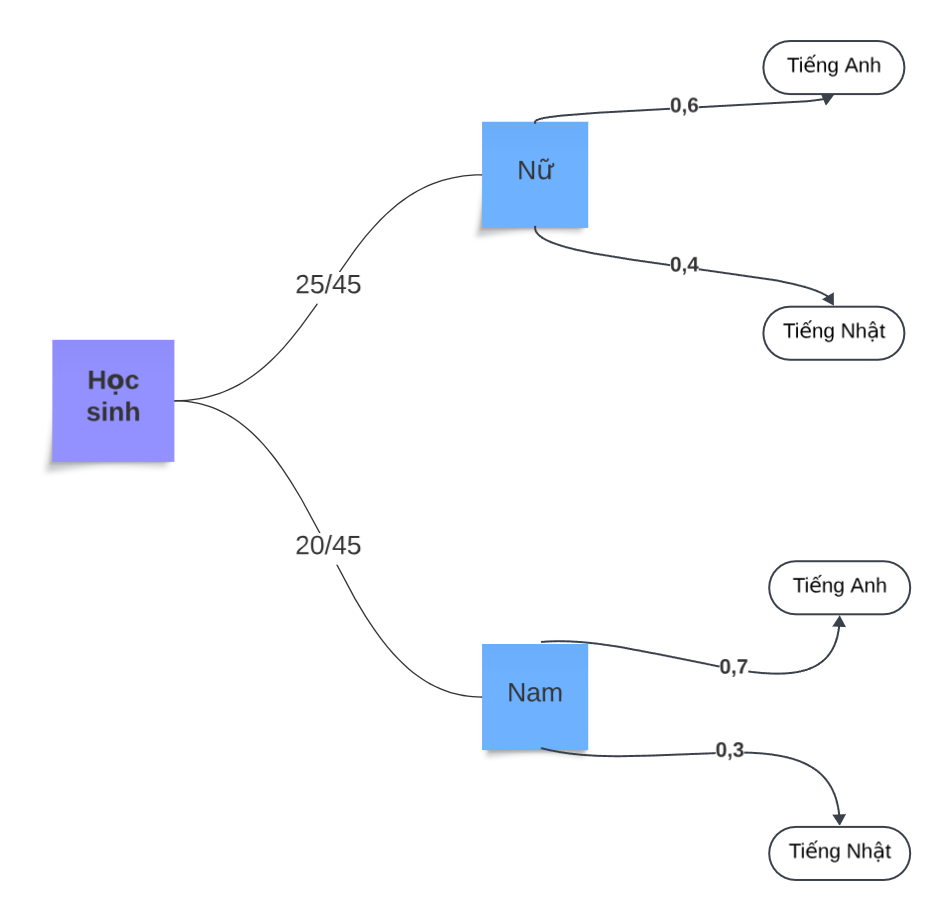
A: “Bạn được chọn là nam và học tiếng Nhật”;

B: “Bạn được chọn là nữ và học tiếng Anh”.

Xác suất bạn được chọn là nam và học tiếng Nhật:

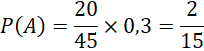
Xác suất bạn được chọn là nữ và học tiếng Anh:

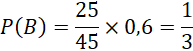
Bài 4 trang 75 toán 12 tập 2 ctst 

Máy tính và thiết bị lưu điện (UPS) được kết nối như Hình 5. Khi xảy ra sự cố điện, UPS bị hỏng với xác suất 0,02. Nếu UPS bị hỏng khi xảy ra sự cố điện, máy tính sẽ bị hỏng với xác suất 0,1; ngược lại, nếu UPS không bị hỏng, máy tính sẽ không bị hỏng.

a) Tính xác suất để cả UPS và máy tính đều không bị hỏng khi xảy ra sự cố điện.

b) Tính xác suất để cả UPS và máy tính đều bị hỏng khi xảy ra sự cố điện.

Giải nhanh:

a) 0,98

b) 0,002