BÀI 3. TÍCH CỦA MỘT SỐ VỚI MỘT VECTO

PHẦN I: HỆ THỐNG BÀI TẬP CUỐI SGK

Bài 1. Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a. + + + = 4

b. + + = 2

Bài 2. Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:

a.

b.

Bài 3. Cho hai điểm phân biệt A và B. Xác định điểm M sao cho

Bài 4. Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng

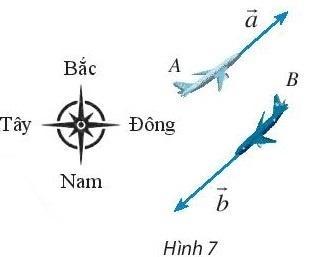
Bài 5. Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800km/h. Biểu diễn vectơ vận tốc  của máy bay B theo vectơ vận tốc   của máy bay A.

Bài 6. Cho hai điểm phân biệt A và B.

a. Xác định điểm O sao cho

b. Chứng minh rằng với mọi điểm M, ta có

Bài 7. Cho tam giác ABC.

a. Xác định điểm M, N thảo mãn

b. Biểu thị mỗi vectơ theo hai vectơ         

c. Chứng minh ba điểm M, N, P thẳng hàng.

PHẦN II: 5 PHÚT GIẢI BÀI TẬP CUỐI SGK

Bài 1. 

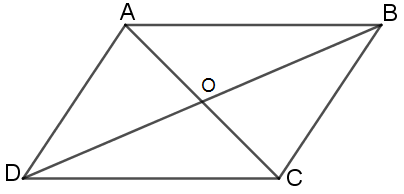
a. Ta có: O là giao điểm hai đường chéo của hình bình hành ABCD 

+ + + = + + + = 4 (đpcm)

b.Ta có:   + =

+ + = 2 (đpcm)

Bài 2. 

a. VT= (đpcm)

b. Giả sử: =>

 => => (luôn đúng)

Vậy

Bài 3. 

Điểm M nằm giữa A và B và

Bài 4. 

VT=

= + + + + + + +

= 2 + ( + ) + 2 + ( + ) = 2 + + 2 +  

= 2( + ) = 2( + + + )

= 4 + 2. = 4 = VP (đpcm)

Bài 5. 

=

Bài 6. 

a. O trên đoạn thẳng AB sao cho OA = 3OB

b. Ta có: =>

=> (đpcm)

Bài 7. 

a)

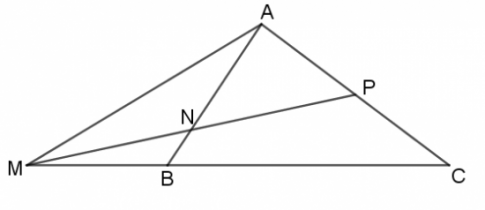
b) = + ; = +

c) Theo phần b, ta thấy: = 2  nên ba điểm M, N, P thẳng hàng.