CHƯƠNG V. VECTƠ

BÀI 3. TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ

1. TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ VÀ CÁC TÍNH CHẤT

HĐKP1:

+ |$\underset{a}{\rightarrow}$ + $\underset{a}{\rightarrow}$| = 2|$\underset{a}{\rightarrow}$|, vectơ $\underset{a}{\rightarrow}$ + $\underset{a}{\rightarrow}$ cùng hướng với vectơ $\underset{a}{\rightarrow}$

+  (-$\underset{a}{\rightarrow}$)+(-$\underset{a}{\rightarrow}$) = 2|-$\underset{a}{\rightarrow}$|, vectơ (-$\underset{a}{\rightarrow}$) + (-$\underset{a}{\rightarrow}$) ngược hướng với.

Kết luận:

Cho số k khác 0 và vectơ $\underset{a}{\rightarrow}$ khác $\underset{0}{\rightarrow}$ . Tích của số k với vectơ, kí hiệu là k $\underset{a}{\rightarrow}$.

Vectơ k$\underset{a}{\rightarrow}$ cùng hướng với $\underset{a}{\rightarrow}$ nếu k > 0, ngược hướng với $\underset{a}{\rightarrow}$ nếu k>0, ngược hướng với $\underset{a}{\rightarrow}$ nếu k < 0 và có độ dài bằng |k|.|$\underset{a}{\rightarrow}$|.

Ta quy ước 0$\underset{a}{\rightarrow}$ = $\underset{0}{\rightarrow}$ và k$\underset{0}{\rightarrow}$ =$\underset{0}{\rightarrow}$.

Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.

Ví dụ 1: SGK-tr94

Kết luận:

Với hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ bất kì, với mọi số thực h và k, ta có:

Ví dụ 2: SGK-tr95

Ví dụ 3: SGK-tr95

Thực hành 1.

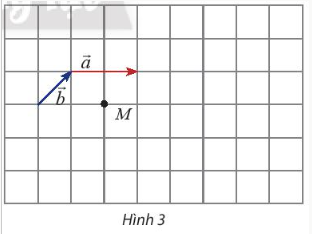
a)

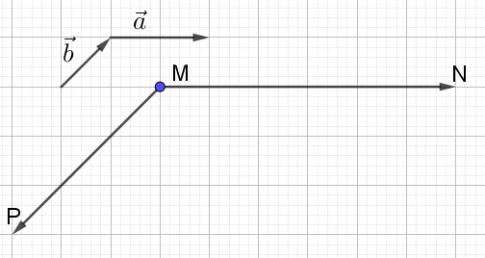
b) |3$\underset{b}{\rightarrow}$| = |-3$\underset{b}{\rightarrow}$| = 3$\sqrt{2}$

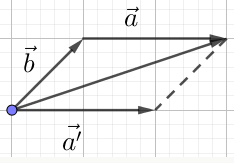
Ta có: |2$\underset{a}{\rightarrow}$+ 2$\underset{b}{\rightarrow}$|  = 2|$\underset{a}{\rightarrow}$+ $\underset{b}{\rightarrow}$|= 2|$\underset{a'}{\rightarrow}$+ $\underset{b}{\rightarrow}$|

= 2$\sqrt{2^{2}+(\sqrt{2})^{2}+2.2.\sqrt{2}.cos45^{\circ}}$=$\sqrt{10}$

Thực hành 2.

G là trọng tâm tam giác ABC 

<=> $\underset{GA}{\rightarrow}$ + $\underset{GB}{\rightarrow}$ + $\underset{GC}{\rightarrow}$ = $\underset{0}{\rightarrow}$

$\underset{MA}{\rightarrow}$- $\underset{MG}{\rightarrow}$ + $\underset{MB}{\rightarrow}$ - $\underset{MG}{\rightarrow}$ + $\underset{MC}{\rightarrow}$ - $\underset{MG}{\rightarrow}$ = $\underset{0}{\rightarrow}$

$\underset{MA}{\rightarrow}$+ $\underset{MB}{\rightarrow}$ + $\underset{MC}{\rightarrow}$ - 3$\underset{MG}{\rightarrow}$ = $\underset{0}{\rightarrow}$

$\underset{MA}{\rightarrow}$ + $\underset{MB}{\rightarrow}$ + $\underset{MC}{\rightarrow}$ = 3$\underset{MG}{\rightarrow}$ (đpcm)

Vận dụng.

$\underset{b}{\rightarrow}$ = -$\frac{5}{2} \underset{a}{\rightarrow}$

2. ĐIỀU KIỆN ĐỂ HAI VECTƠ CÙNG PHƯƠNG 

HĐKP 2:

Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{c}{\rightarrow}$ cùng hướng với nhau.

⇒ Kết luận:

Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ ($\underset{b}{\rightarrow} \neq  \underset{0}{\rightarrow}$) cùng phương khi và chỉ khi có số k sao cho $\underset{a}{\rightarrow}$=k$\underset{b}{\rightarrow}$

Nhận xét:

Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để $\underset{AB}{\rightarrow}$=k$\underset{AC}{\rightarrow}$.

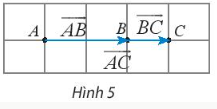
Ví dụ 4: SGK – tr96

* Chú ý:

Cho hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ không cùng phương. Với mỗi vectơ $\underset{c}{\rightarrow}$ luôn tồn tại duy nhất cặp số thực (m;n) sao cho $\underset{c}{\rightarrow}$=m.$\underset{a}{\rightarrow}$+n.$\underset{b}{\rightarrow}$

Thực hành 3.

Ta có: $\underset{GA}{\rightarrow}$ + $\underset{GB}{\rightarrow}$ + $\underset{GC}{\rightarrow}$ + $\underset{GD}{\rightarrow}$ = $\underset{0}{\rightarrow}$

$\underset{IA}{\rightarrow}$ - $\underset{IG}{\rightarrow}$ + $\underset{IB}{\rightarrow}$ - $\underset{IG}{\rightarrow}$ + $\underset{JC}{\rightarrow}$ - $\underset{JG}{\rightarrow}$ +  $\underset{JD}{\rightarrow}$- $\underset{JG}{\rightarrow}$ = $\underset{0}{\rightarrow}$

($\underset{IA}{\rightarrow}$ + $\underset{IB}{\rightarrow}$) - 2$\underset{IG}{\rightarrow}$ + ($\underset{JC}{\rightarrow}$ + $\underset{JD}{\rightarrow}$) - 2$\underset{JG}{\rightarrow}$ = $\underset{0}{\rightarrow}$

$\underset{0}{\rightarrow}$ - 2$\underset{IG}{\rightarrow}$ + $\underset{0}{\rightarrow}$ - 2$\underset{JG}{\rightarrow}$ = $\underset{0}{\rightarrow}$ ( vì I, J là trung điểm của AB, DC)

$\underset{IG}{\rightarrow}$ = - JG

Ba điểm I, J, G thẳng hàng (đpcm).